Residue form
A generalization of the concept of a residue of an analytic function of one complex variable to several complex variables. Let  be a complex-analytic manifold (cf. Analytic manifold), let
be a complex-analytic manifold (cf. Analytic manifold), let 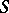 be an analytic submanifold of complex codimension one and let
be an analytic submanifold of complex codimension one and let 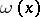 be a closed exterior differential form of class
be a closed exterior differential form of class 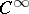 on
on  with a first-order polar singularity on
with a first-order polar singularity on 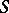 . The last condition means that for a function
. The last condition means that for a function 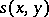 , holomorphic with respect to
, holomorphic with respect to  in a neighbourhood
in a neighbourhood 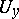 of a point
of a point 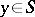 and such that
and such that
 |
the form 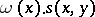 belongs to the class
belongs to the class 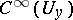 . Under these conditions there exist, in a neighbourhood
. Under these conditions there exist, in a neighbourhood 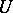 of an arbitrary point
of an arbitrary point 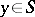 , forms
, forms 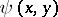 ,
,  of class
of class 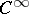 such that
such that
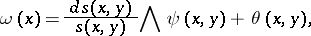 |
where 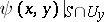 is a closed form of class
is a closed form of class 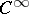 that depends only on
that depends only on 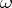 . The closed form on
. The closed form on 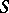 which is defined in a neighbourhood of any point
which is defined in a neighbourhood of any point 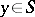 by the restriction
by the restriction 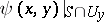 , is called the residue form of
, is called the residue form of 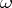 , and is denoted by
, and is denoted by
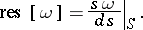 |
If the form 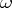 is holomorphic, its residue form is holomorphic as well (cf. Holomorphic form). For instance, for
is holomorphic, its residue form is holomorphic as well (cf. Holomorphic form). For instance, for 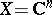 ,
, 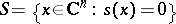 and the form
and the form
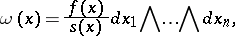 |
where 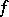 and
and  are holomorphic functions in
are holomorphic functions in 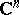 ,
, 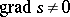 on
on 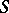 , the residue form is
, the residue form is
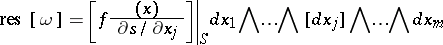 |
at the points where 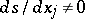 .
.
The residue formula corresponding to residue forms is:
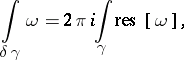 |
where  is an arbitrary cycle in
is an arbitrary cycle in 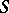 of dimension equal to the degree of
of dimension equal to the degree of 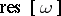 and
and 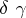 — a cycle in
— a cycle in 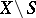 — is the boundary of some chain in
— is the boundary of some chain in 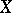 in general position with
in general position with 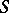 and intersecting
and intersecting 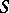 along
along 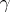 .
.
The composite residue form 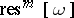 is defined by induction.
is defined by induction.
The residue class of a closed form 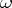 in
in 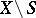 is the cohomology class on the submanifold
is the cohomology class on the submanifold 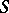 produced by the residue forms of the forms of class
produced by the residue forms of the forms of class 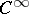 in
in 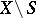 that are cohomologous with
that are cohomologous with 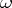 and have a first-order polar singularity on
and have a first-order polar singularity on 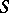 . The residue class of a form
. The residue class of a form 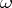 is denoted by
is denoted by 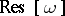 . The residue class of a holomorphic form need not contain a holomorphic form, since in the general case it is not permissible to restrict the considerations to the ring of holomorphic forms but one rather has to consider the ring of closed forms. It is possible, however, if
. The residue class of a holomorphic form need not contain a holomorphic form, since in the general case it is not permissible to restrict the considerations to the ring of holomorphic forms but one rather has to consider the ring of closed forms. It is possible, however, if 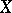 is a Stein manifold. The residue class
is a Stein manifold. The residue class 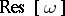 does not depend on the choice of
does not depend on the choice of 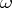 out of one cohomology class and realizes a homomorphism from the group of cohomology classes of the manifold
out of one cohomology class and realizes a homomorphism from the group of cohomology classes of the manifold 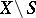 to the group of cohomology classes of the manifold
to the group of cohomology classes of the manifold 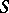 :
:
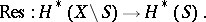 |
As for residue forms, the following residue formula is valid:
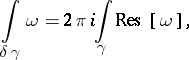 |
and the integral on the right-hand side of this equation is taken over any form in the residue class 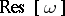 and is independent of it.
and is independent of it.
For references, see (, ,
to) Residue of an analytic function.
Comments
A differential form whose coefficients are distributions (generalized functions) is called a current. The theory of currents was developed largely by H. Federer [a5]. One can define the residue of a current. Currents associated to complex-analytic varieties have attracted a great deal of attention, see, e.g., [a6]–[a8].
Residue forms are also called residue currents. As mentioned above, these arise as generalizations to several variables of the residue, or rather the principal part, of an analytic function. There are several other ways of looking at residues: Let 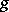 be holomorphic on a bounded domain
be holomorphic on a bounded domain 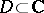 except for a (finite) set of singularities
except for a (finite) set of singularities 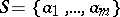 . Let
. Let 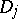 be a neighbourhood of
be a neighbourhood of 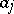 with smooth boundary,
with smooth boundary, 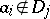 if
if 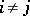 . Let
. Let 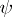 be smooth, compactly supported on
be smooth, compactly supported on  and holomorphic in a neighbourhood of
and holomorphic in a neighbourhood of 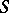 , then
, then
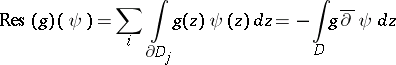 | (a1) |
is independent of 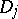 as long as the
as long as the 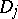 are contained in the neighbourhood of
are contained in the neighbourhood of 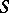 where
where 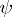 is holomorphic. If one takes for
is holomorphic. If one takes for 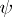 a function that equals
a function that equals 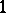 in a small neighbourhood of
in a small neighbourhood of 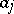 , one obtains the usual residue. Note that
, one obtains the usual residue. Note that 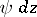 represents a germ of a
represents a germ of a 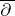 -closed
-closed 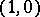 -form at
-form at 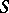 and
and 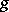 is a
is a 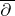 -closed
-closed  -form. Thus
-form. Thus  . Here
. Here 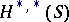 denotes Dolbeault cohomology of germs of forms at
denotes Dolbeault cohomology of germs of forms at 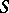 .
. 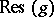 is called the cohomological residue. This can be generalized to several variables,
is called the cohomological residue. This can be generalized to several variables, 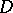 will be a domain in
will be a domain in 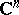 ,
, 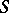 a closed subvariety of
a closed subvariety of  , to obtain a homomorphism
, to obtain a homomorphism
 |
In another direction one would like to have an interpretation of (a1) for smooth 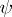 , not necessarily closed. This can be done if one imposes the condition that
, not necessarily closed. This can be done if one imposes the condition that 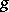 is meromorphic on
is meromorphic on 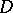 . One may write
. One may write 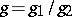 , with
, with 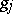 holomorphic, and assume by a partition of unity that
holomorphic, and assume by a partition of unity that 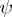 is supported on
is supported on 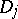 only. Then the following limit exists independently of the representation of
only. Then the following limit exists independently of the representation of 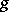 :
:
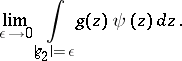 | (a2) |
It defines a current supported on 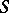 . To obtain a sensible analogue of this for several variables is much harder.
. To obtain a sensible analogue of this for several variables is much harder.
A semi-meromorphic form on 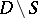 is a smooth differential form
is a smooth differential form 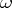 on
on 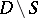 that for every point
that for every point 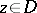 admits a holomorphic function
admits a holomorphic function 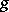 defined on some neighbourhood of
defined on some neighbourhood of  such that
such that 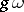 is smooth at
is smooth at  . A good generalization of (a2) should yield "residues" of a semi-meromorphic
. A good generalization of (a2) should yield "residues" of a semi-meromorphic 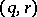 -form
-form 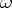 , which should be currents supported on
, which should be currents supported on 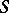 . One needs the existence of limits of the form
. One needs the existence of limits of the form
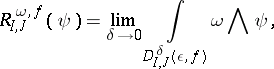 |
with
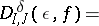 |
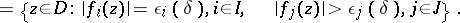 |
Here 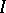 and
and 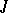 are disjoint subsets of
are disjoint subsets of 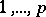 ,
, 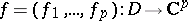 is a holomorphic mapping with
is a holomorphic mapping with  ,
, 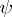 is an arbitrary compactly-supported smooth
is an arbitrary compactly-supported smooth 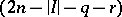 -form and
-form and 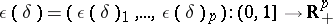 is an admissible path, that is,
is an admissible path, that is, 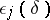 and
and 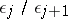 tend to
tend to  with
with 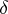 . In fact, the
. In fact, the 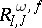 are
are 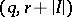 -currents. For these two approaches, see [a4].
-currents. For these two approaches, see [a4].
A third direction towards residue currents is by analytic continuation of holomorphic current-valued mappings. See [a2].
References
| [a1] | L.A. Aizenberg, A.P. Yuzhakov, "Integral representations and residues in multidimensional complex analysis" , Transl. Math. Monogr. , 58 , Amer. Math. Soc. (1983) (Translated from Russian) |
| [a2] | C.A. Berenstein, R. Gay, A. Yger, "Analytic continuation of currents and division problems" Forum Math. (1989) pp. 15–51 |
| [a3] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
| [a4] | M. Passare, "Residues, currents and their relation to ideals of holomorphic functions" Math. Scand. , 62 (1988) pp. 75–152 |
| [a5] | H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108 |
| [a6] | R. Harvey, "Holomorphic chains and their boundaries" R.O. Wells jr. (ed.) , Several Complex Variables , Proc. Symp. Pure Math. , 30:1 , Amer. Math. Soc. (1977) pp. 309–382 |
| [a7] | H. Skoda, "A survey of the theory of closed, positive currents" Y.-T. Siu (ed.) , Complex Analysis of Several Variables , Proc. Symp. Pure Math. , 41 , Amer. Math. Soc. (1984) pp. 181–190 |
| [a8] | E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian) |
Residue form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Residue_form&oldid=14216