Regular space
A topological space in which for every point  and every closed set
and every closed set  not containing
not containing  there are open disjoint sets
there are open disjoint sets  and
and  such that
such that  and
and  . A completely-regular space and, in particular, a metric space are regular.
. A completely-regular space and, in particular, a metric space are regular.
If all one-point subsets in a regular space are closed (and this is not always true!), then the space is called a  -space. Not every regular space is completely regular: there is an infinite
-space. Not every regular space is completely regular: there is an infinite 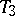 -space on which every continuous real-valued function is constant. Moreover, not every regular space is normal (cf. Normal space). However, if a space is regular and each of its open coverings contains a countable subcovering, then it is normal. A space with a countable base is metrizable if and only if it is a
-space on which every continuous real-valued function is constant. Moreover, not every regular space is normal (cf. Normal space). However, if a space is regular and each of its open coverings contains a countable subcovering, then it is normal. A space with a countable base is metrizable if and only if it is a 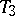 -space. Regularity is inherited by any subspace and is multiplicative.
-space. Regularity is inherited by any subspace and is multiplicative.
References
| [1] | J.L. Kelley, "General topology" , Springer (1975) |
| [2] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
Comments
See also Separation axiom for the hierarchy of 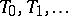 . A topological property is said to be multiplicative if the product space
. A topological property is said to be multiplicative if the product space 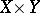 has it if both
has it if both  and
and  have the property. This is not to be confused with a "multiplicative system of subsetsmultiplicative system of subsets" , a phrase that is sometimes used to denote a collection of subsets that is closed under finite intersections.
have the property. This is not to be confused with a "multiplicative system of subsetsmultiplicative system of subsets" , a phrase that is sometimes used to denote a collection of subsets that is closed under finite intersections.
References
| [a1] | E. Čech, "Topological spaces" , Wiley (1966) pp. 492ff |
Regular space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_space&oldid=11451