Regular group
There are several (different) notions of regularity in group theory. Most are not intrinsic to a group itself, but pertain to a group acting on something.
Regular group of permutations.
Let 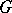 be a finite group acting on a set
be a finite group acting on a set  , i.e. a permutation group (group of permutations). The permutation group
, i.e. a permutation group (group of permutations). The permutation group 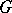 is said to be regular if for all
is said to be regular if for all 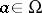 ,
, 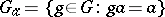 , the stabilizer subgroup at
, the stabilizer subgroup at  , is trivial.
, is trivial.
In the older mathematical literature, and in physics, a slightly stronger notion is used: 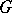 is transitive (i.e., for all
is transitive (i.e., for all 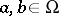 there is a
there is a 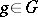 such that
such that 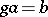 ) and
) and 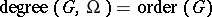 , where
, where 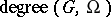 is the number of elements of
is the number of elements of  and
and 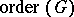 is, of course, the number of elements of
is, of course, the number of elements of 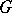 . It is easy to see that a transitive regular permutation group satisfies this condition. Inversely, a transitive permutation group for which
. It is easy to see that a transitive regular permutation group satisfies this condition. Inversely, a transitive permutation group for which 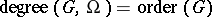 is regular.
is regular.
A permutation is regular if all cycles in its canonical cycle decomposition have the same length. If 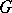 is a transitive regular permutation group, then all its elements, regarded as permutations on
is a transitive regular permutation group, then all its elements, regarded as permutations on  , are regular permutations.
, are regular permutations.
An example of a transitive regular permutation group is the Klein 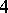 -group
-group  of permutations of
of permutations of 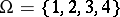 .
.
The regular permutation representation of a group  defined by left (respectively, right) translation
defined by left (respectively, right) translation 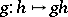 (respectively,
(respectively, 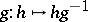 ) exhibits
) exhibits 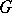 as a regular permutation group on
as a regular permutation group on 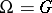 .
.
Regular group of automorphisms.
Let 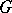 act on a group
act on a group 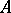 by means of automorphisms (i.e., there is given a homomorphism of groups
by means of automorphisms (i.e., there is given a homomorphism of groups 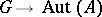 ,
, 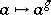 ,
, 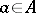 ).
). 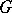 is said to act fixed-point-free if for all
is said to act fixed-point-free if for all 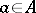 there is a
there is a 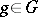 such that
such that 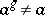 , i.e. there is no other global fixed point except the obvious and necessary one
, i.e. there is no other global fixed point except the obvious and necessary one  . There is a conjecture that if
. There is a conjecture that if 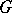 acts fixed-point-free on
acts fixed-point-free on  and
and 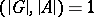 , then
, then  is solvable, [a7]; see also Fitting length for some detailed results in this direction.
is solvable, [a7]; see also Fitting length for some detailed results in this direction.
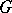 is said to be a regular group of automorphisms of
is said to be a regular group of automorphisms of 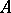 if for all
if for all 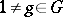 only the identity element of
only the identity element of 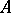 is left fixed by
is left fixed by 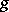 , i.e.
, i.e.  for all
for all 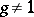 . Some authors use the terminology "fixed-point-free" for the just this property.
. Some authors use the terminology "fixed-point-free" for the just this property.
Regular 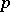 -group.
-group.
A  -group is said to be regular if
-group is said to be regular if  , where
, where  is an element of the commutator subgroup of the subgroup generated by
is an element of the commutator subgroup of the subgroup generated by  and
and  , i.e.
, i.e.  is a product of iterated commutators of
is a product of iterated commutators of  and
and 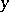 . See [a5].
. See [a5].
References
| [a1] | K. Doerk, T. Hawkes, "Finite soluble groups" , de Gruyter (1992) pp. 16 |
| [a2] | W. Ledermann, A.J. Weir, "Introduction to group theory" , Longman (1996) pp. 125 (Edition: Second) |
| [a3] | M. Hall Jr., "The theory of groups" , Macmillan (1963) pp. 183 |
| [a4] | M. Hamermesh, "Group theory and its applications to physical problems" , Dover, reprint (1989) pp. 19 |
| [a5] | R.D. Carmichael, "Groups of finite order" , Dover, reprint (1956) pp. 54ff |
| [a6] | L. Dornhoff, "Group representation theory. Part A" , M. Dekker (1971) pp. 65 |
| [a7] | B. Huppert, N. Blackburn, "Finite groups III" , Springer (1982) pp. Chap. X |
Regular group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_group&oldid=11804