Regular element

of a semi-group

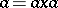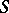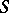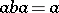An element such that for some element of the given semi-group; if in addition (for the same ) , then is called completely regular. If is a regular element of a semi-group , then the principal right (left) ideal in generated by is generated by some idempotent; conversely, each of these symmetrical properties implies the regularity of . If and 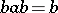, the elements and 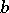are called mutually inverse (also known as generalized inverse or regularly conjugate). Every regular element has an element inverse to it; generally speaking, it is not unique (see Inversion semi-group). Semi-groups in which any two elements are mutually inverse are in fact rectangular semi-groups (see Idempotents, semi-group of). Each completely-regular element has an element inverse to it that commutes with . An element is completely regular if and only if it belongs to some subgroup of a semi-group (cf. Clifford semi-group). For regular -classes, see Green equivalence relations.

References

[1]	A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967)
[2]	E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian)

Comments

A semi-group consisting completely of regular elements is a regular semi-group.