Regular boundary point
A point 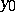 on the boundary
on the boundary 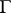 of a domain
of a domain 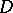 in a Euclidean space
in a Euclidean space 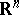 ,
, 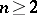 , at which, for any continuous function
, at which, for any continuous function 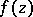 on
on 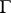 , the generalized solution
, the generalized solution 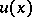 of the Dirichlet problem in the sense of Wiener–Perron (see Perron method) takes the boundary value
of the Dirichlet problem in the sense of Wiener–Perron (see Perron method) takes the boundary value 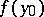 , that is,
, that is,
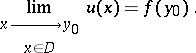 |
The regular boundary points of 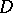 form a set
form a set 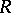 , at the points of which the complement
, at the points of which the complement 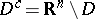 is not a thin set; the set
is not a thin set; the set 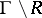 of irregular boundary points (cf. Irregular boundary point) is a polar set of type
of irregular boundary points (cf. Irregular boundary point) is a polar set of type 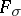 . If all points of
. If all points of 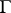 are regular boundary points, then the domain
are regular boundary points, then the domain 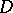 is called regular with respect to the Dirichlet problem.
is called regular with respect to the Dirichlet problem.
For 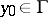 to be a regular boundary point it is necessary and sufficient that in the intersection
to be a regular boundary point it is necessary and sufficient that in the intersection 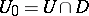 of
of 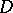 with any neighbourhood
with any neighbourhood 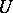 of
of  there is a superharmonic barrier (a function
there is a superharmonic barrier (a function 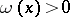 in
in 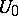 such that
such that 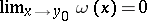 , Lebesgue's criterion for a barrier). It was first shown by H. Lebesgue in 1912 that for
, Lebesgue's criterion for a barrier). It was first shown by H. Lebesgue in 1912 that for 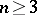 the vertex of a sufficiently acute angle lying in
the vertex of a sufficiently acute angle lying in 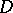 need not be a regular boundary point.
need not be a regular boundary point.
Let
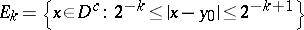 |
and let 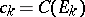 be the capacity of the set
be the capacity of the set 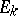 . For
. For 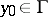 to be a regular boundary point it is necessary and sufficient that the series
to be a regular boundary point it is necessary and sufficient that the series
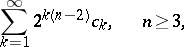 |
diverges, or for 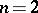 , that the series
, that the series
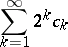 |
diverges, where
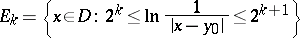 |
(Wiener's criterion).
For 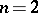 , a point
, a point 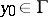 is a regular boundary point if there is a continuous path
is a regular boundary point if there is a continuous path 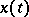 ,
, 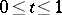 , such that
, such that 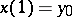 , and
, and 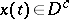 for
for 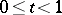 . When
. When 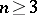 , a point
, a point 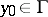 is a regular boundary point if it can be reached by the vertex of a right circular cone belonging to
is a regular boundary point if it can be reached by the vertex of a right circular cone belonging to  in a sufficiently small neighbourhood of
in a sufficiently small neighbourhood of  . In the case of a domain
. In the case of a domain 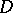 in the compactified space
in the compactified space 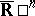 ,
, 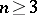 , the point at infinity
, the point at infinity 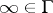 is always a regular boundary point; when
is always a regular boundary point; when 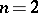 , the point at infinity
, the point at infinity 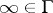 is a regular boundary point if there is a continuous path
is a regular boundary point if there is a continuous path 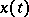 ,
, 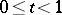 , such that
, such that 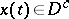 for
for 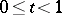 , and
, and 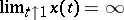 .
.
References
| [1] | M.V. Keldysh, "On the solvability and stability of the Dirichlet problem" Uspekhi Mat. Nauk , 8 (1941) pp. 171–232 (In Russian) |
| [2] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [3] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Acad. Press (1976) |
Comments
The polarity of the set of irregular boundary points is contained in the Kellogg–Evans theorem. See, e.g., [a1] for irregular boundary points in abstract potential theory.
References
| [a1] | J. Bliedtner, W. Hansen, "Potential theory. An analytic and probabilistic approach to balayage" , Springer (1986) |
| [a2] | H. Lebesgue, "Sur des cas d'impossibilité du problème de Dirichlet ordinaire" C.R. Séances Soc. Math. France , 41 (1913) pp. 17 |
| [a3] | H. Lebesgue, "Conditions de régularité, conditions d'irrégularité, conditions d'impossibilité dans le problème de Dirichlet" C.R. Acad. Sci. Paris , 178 (1924) pp. 349–354 |
| [a4] | N. Wiener, "The Dirichlet problem" J. Math. Phys. , 3 (1924) pp. 127–146 |
| [a5] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
| [a6] | J. Wermer, "Potential theory" , Lect. notes in math. , 408 , Springer (1981) |
Regular boundary point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_boundary_point&oldid=15319