Reflection of an object of a category
reflector of an object of a category
Let 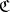 be a subcategory of a category
be a subcategory of a category 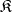 ; an object
; an object  is called a reflection of an object
is called a reflection of an object 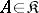 in
in 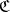 , or a
, or a 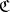 -reflection, if there exists a morphism
-reflection, if there exists a morphism 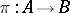 such that for any object
such that for any object 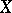 of
of 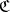 the mapping
the mapping
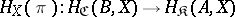 |
is bijective. In other words, for any morphism 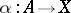 there is a unique morphism
there is a unique morphism 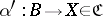 such that
such that 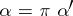 . A
. A 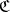 -reflection of an object
-reflection of an object 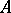 is not uniquely defined, but any two
is not uniquely defined, but any two 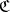 -reflections of an object
-reflections of an object 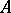 are isomorphic. The
are isomorphic. The 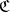 -reflection of an initial object of
-reflection of an initial object of 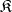 is an initial object in
is an initial object in 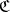 . The left adjoint of the inclusion functor
. The left adjoint of the inclusion functor 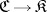 (if it exists), i.e. the functor assigning to an object of
(if it exists), i.e. the functor assigning to an object of 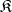 its reflection in
its reflection in 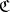 , is called a reflector.
, is called a reflector.
Examples. In the category of groups the quotient group 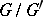 of an arbitrary group
of an arbitrary group  by its commutator subgroup is a reflection of
by its commutator subgroup is a reflection of 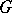 in the subcategory of Abelian groups. For an Abelian group
in the subcategory of Abelian groups. For an Abelian group  , the quotient group
, the quotient group  by its torsion subgroup
by its torsion subgroup 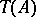 is a reflection of
is a reflection of  in the full subcategory of torsion-free Abelian groups. The injective hull
in the full subcategory of torsion-free Abelian groups. The injective hull 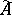 of the group
of the group  is a reflection of the groups
is a reflection of the groups 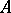 and
and  in the subcategory of full torsion-free Abelian groups.
in the subcategory of full torsion-free Abelian groups.
Reflections are usually examined in full subcategories. A full subcategory 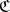 of a category
of a category 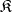 in which there are reflections for all objects of
in which there are reflections for all objects of 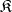 is called reflective (cf. Reflexive category).
is called reflective (cf. Reflexive category).
Comments
The reflection of an object solves a universal problem (cf. Universal problems).
Reflection of an object of a category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reflection_of_an_object_of_a_category&oldid=16715