Reductive group
A linear algebraic group 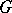 (over an algebraically closed field
(over an algebraically closed field 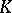 ) that satisfies one of the following equivalent conditions: 1) the radical of the connected component
) that satisfies one of the following equivalent conditions: 1) the radical of the connected component 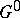 of the unit element of
of the unit element of 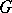 is an algebraic torus; 2) the unipotent radical of the group
is an algebraic torus; 2) the unipotent radical of the group 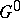 is trivial; or 3) the group
is trivial; or 3) the group 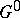 is a product of closed normal subgroups
is a product of closed normal subgroups 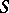 and
and 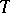 that are a semi-simple algebraic group and an algebraic torus, respectively. In this case
that are a semi-simple algebraic group and an algebraic torus, respectively. In this case 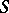 is the commutator subgroup of
is the commutator subgroup of 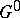 and
and 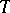 coincides with the radical of
coincides with the radical of 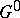 as well as with the connected component of the unit element of its centre;
as well as with the connected component of the unit element of its centre; 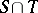 is finite, and any semi-simple or unipotent subgroup of the group
is finite, and any semi-simple or unipotent subgroup of the group 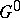 is contained in
is contained in 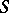 .
.
A linear algebraic group 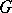 is called linearly reductive if either of the two following equivalent conditions is fulfilled: a) each rational linear representation of
is called linearly reductive if either of the two following equivalent conditions is fulfilled: a) each rational linear representation of 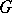 is completely reducible (cf. Reducible representation); or b) for each rational linear representation
is completely reducible (cf. Reducible representation); or b) for each rational linear representation 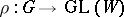 and any
and any 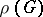 -invariant vector
-invariant vector 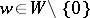 there is a
there is a 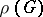 -invariant linear function
-invariant linear function 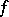 on
on 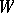 such that
such that 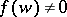 . Any linearly reductive group is reductive. If the characteristic of the field
. Any linearly reductive group is reductive. If the characteristic of the field 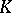 is 0, the converse is true. This is not the case when
is 0, the converse is true. This is not the case when 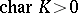 : A connected linearly reductive group is an algebraic torus. However, even in the general case, a reductive group can be described in terms of its representation theory. A linear algebraic group
: A connected linearly reductive group is an algebraic torus. However, even in the general case, a reductive group can be described in terms of its representation theory. A linear algebraic group 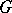 is called geometrically reductive (or semi-reductive) if for each rational linear representation
is called geometrically reductive (or semi-reductive) if for each rational linear representation 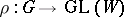 and any
and any 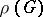 -invariant vector
-invariant vector 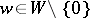 there is a non-constant
there is a non-constant 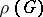 -invariant polynomial function
-invariant polynomial function 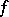 on
on 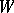 such that
such that  . A linear algebraic group is reductive if and only if it is geometrically reductive (see Mumford hypothesis).
. A linear algebraic group is reductive if and only if it is geometrically reductive (see Mumford hypothesis).
The generalized Hilbert theorem on invariants is true for reductive groups. The converse is also true: If 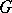 is a linear algebraic group over an algebraically closed field
is a linear algebraic group over an algebraically closed field 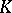 and if for any locally finite-dimensional rational representation by automorphisms of a finitely-generated associative commutative
and if for any locally finite-dimensional rational representation by automorphisms of a finitely-generated associative commutative 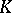 -algebra
-algebra 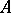 with identity the algebra of invariants
with identity the algebra of invariants 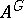 is finitely generated, then
is finitely generated, then 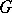 is reductive (see [4]).
is reductive (see [4]).
Any finite linear group is reductive and if its order is not divisible by  , then it is also linearly reductive. Connected reductive groups have a structure theory that is largely similar to the structure theory of reductive Lie algebras (root system; Weyl group, etc., see [2]). This theory extends to groups
, then it is also linearly reductive. Connected reductive groups have a structure theory that is largely similar to the structure theory of reductive Lie algebras (root system; Weyl group, etc., see [2]). This theory extends to groups 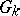 where
where 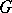 is a connected reductive group defined over a subfield
is a connected reductive group defined over a subfield 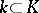 and
and 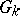 is the group of its
is the group of its 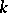 -rational points (see [3]). In this case the role of Borel subgroups (cf. Borel subgroup), maximal tori (cf. Maximal torus) and Weyl groups is played by minimal parabolic subgroups (cf. Parabolic subgroup) defined over
-rational points (see [3]). In this case the role of Borel subgroups (cf. Borel subgroup), maximal tori (cf. Maximal torus) and Weyl groups is played by minimal parabolic subgroups (cf. Parabolic subgroup) defined over 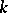 , maximal tori split over
, maximal tori split over 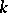 , and relative Weyl groups (see Weyl group), respectively. Any two minimal parabolic subgroups of
, and relative Weyl groups (see Weyl group), respectively. Any two minimal parabolic subgroups of 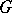 that are defined over
that are defined over 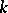 are conjugate by an element of
are conjugate by an element of 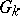 ; this is also true for any two maximal
; this is also true for any two maximal 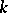 -split tori of
-split tori of 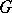 .
.
If 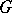 is a connected reductive group defined over a field
is a connected reductive group defined over a field 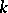 , then
, then 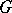 is a split group over a separable extension of finite degree of
is a split group over a separable extension of finite degree of 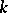 ; if, in addition,
; if, in addition,  is an infinite field, then
is an infinite field, then 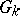 is dense in
is dense in 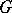 in the Zariski topology. If
in the Zariski topology. If 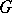 is a reductive group and
is a reductive group and 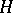 is a closed subgroup of it, then the quotient space
is a closed subgroup of it, then the quotient space 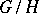 is affine if and only if
is affine if and only if 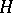 is reductive. A linear algebraic group over a field of characteristic 0 is reductive if and only if its Lie algebra is a reductive Lie algebra (cf. Lie algebra, reductive). If
is reductive. A linear algebraic group over a field of characteristic 0 is reductive if and only if its Lie algebra is a reductive Lie algebra (cf. Lie algebra, reductive). If 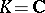 , this is also equivalent to
, this is also equivalent to 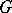 being the complexification of a compact Lie group (see Complexification of a Lie group).
being the complexification of a compact Lie group (see Complexification of a Lie group).
References
| [1] | T.A. Springer, "Invariant theory" , Lect. notes in math. , 585 , Springer (1977) |
| [2] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
| [3] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 |
| [4] | V.L. Popov, "Hilbert's theorem on invariants" Soviet Math. Dokl. , 20 : 6 (1979) pp. 1318–1322 Dokl. Akad. Nauk SSSR , 249 : 3 (1979) pp. 551–555 |
Reductive group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reductive_group&oldid=12805