Recursive equivalence type
An equivalence class for the relation of recursive equivalence, i.e. a collection of all subsets of the natural numbers each of which can be mapped to the other by a bijective partial recursive function. Thus, the concept of a recursive equivalence type serves in recursive set theory as an analogue of the concept of cardinality in classical set theory. Since any two finite sets are recursively equivalent if and only if they contain the same number of elements, the recursive equivalence type of a finite set is completely characterized by the cardinality of this set. This is not the case with infinite sets of natural numbers, despite their equivalence: The collection of all such sets decomposes into a set of the cardinality of the continuum of various recursive equivalence types. Every recursive equivalence type (except the recursive equivalence type of the empty set) is itself a countable set. Sets belonging to one recursive equivalence type are similar in relation to certain algorithmical properties. Thus, the infinite recursively-enumerable sets (cf. Enumerable set) (both the recursive as well as the non-recursive) form a single recursive equivalence type. Since a set that is recursively equivalent to a productive set is itself productive, every recursive equivalence type which contains a productive set consists only of productive sets; this is also the case with immune sets (cf. Immune set). The theory of recursive equivalence types of immune sets, which are known, together with the recursive equivalence types of finite sets, as isols (cf. Isol), has been developed intensively.
Algebraic operations can be defined on recursive equivalence types, the most important of which are addition and multiplication: If  and
and  are recursive equivalence types,
are recursive equivalence types,  ,
,  , and
, and  consists of even numbers while
consists of even numbers while  consists of odd numbers, then
consists of odd numbers, then  is the recursive equivalence type of the set
is the recursive equivalence type of the set  ;
;  is the recursive equivalence type of the set
is the recursive equivalence type of the set  where
where 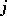 is a general recursive pairing function, one-to-one mapping the Cartesian square of the set of natural numbers onto itself. The algebra of recursive equivalence types is closely connected with the algebra of cardinal numbers, developed without the axiom of choice. The collection of isols is closed with respect to the indicated operations.
is a general recursive pairing function, one-to-one mapping the Cartesian square of the set of natural numbers onto itself. The algebra of recursive equivalence types is closely connected with the algebra of cardinal numbers, developed without the axiom of choice. The collection of isols is closed with respect to the indicated operations.
Attempts have been made to transfer the concept of a recursive equivalence type to classes of sets.
References
| [1] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165 |
| [2] | J.C.E. Dekker, J. Myhill, "Recursive equivalence types" Univ. California Publ. , 3 (1960) pp. 67–213 |
Recursive equivalence type. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursive_equivalence_type&oldid=15449