Rectifiable curve
A curve having a finite length (cf. Line (curve)). Let  be a continuous parametric curve in three-dimensional Euclidean space
be a continuous parametric curve in three-dimensional Euclidean space  , that is,
, that is,  ,
,  , where the
, where the  ,
,  , are continuous functions on the interval
, are continuous functions on the interval  . Let
. Let  be a partition of
be a partition of  and let
and let 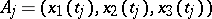 be the sequence of points on
be the sequence of points on 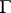 corresponding to
corresponding to  . Also, let
. Also, let 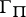 be the polygonal arc inscribed in
be the polygonal arc inscribed in 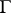 having vertices at
having vertices at 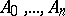 . The length of this arc is
. The length of this arc is
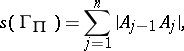 |
where
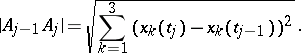 |
Then
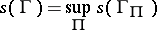 |
is called the length of the curve 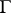 .
. 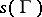 does not depend on the parametrization of
does not depend on the parametrization of 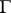 . If
. If 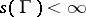 , then
, then  is called a rectifiable curve. A rectifiable curve
is called a rectifiable curve. A rectifiable curve 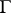 has a tangent at almost every point
has a tangent at almost every point 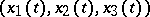 , i.e. for almost all parameter values
, i.e. for almost all parameter values 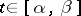 . The study of rectifiable curves was initiated by L. Scheeffer [1] and continued by C. Jordan [2], who proved that
. The study of rectifiable curves was initiated by L. Scheeffer [1] and continued by C. Jordan [2], who proved that 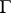 is rectifiable if and only if the functions
is rectifiable if and only if the functions 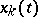 ,
, 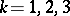 , are of bounded variation on
, are of bounded variation on 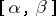 (cf. Function of bounded variation).
(cf. Function of bounded variation).
References
| [1] | L. Scheeffer, "Allgemeine Untersuchungen über Rectification der Curven" Acta Math. , 5 (1885) pp. 49–82 |
| [2] | C. Jordan, "Cours d'analyse" , Gauthier-Villars (1883) |
Comments
All the above works completely similarly for curves in 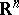 ,
, 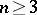 .
.
Rectifiable curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rectifiable_curve&oldid=17729