Rationality theorems
for algebraic groups
Statements about the rationality (unirationality) or non-rationality of various algebraic group varieties (cf. Rational variety, Unirational variety). Since Abelian varieties can never be rational, the main interest is in rationality theorems for linear algebraic groups. Here, the rationality problem has two essentially different features: geometrical and arithmetical, according as whether the ground field  is algebraically closed or not. The first rationality theorems over the field
is algebraically closed or not. The first rationality theorems over the field  of complex numbers were in fact proved by E. Picard and, in contemporary terminology, establish the unirationality of varieties of connected complex groups. The rationality problem for group varieties was clearly stated by C. Chevalley [1] as late as 1954. Progress in this direction is closely connected with achievements in the structure theory of algebraic groups. Thus, the Levi decomposition enables one to reduce the rationality problem to the case of reductive groups, and the Bruhat decomposition is the key to proving the rationality of varieties of reductive groups over any algebraically
of complex numbers were in fact proved by E. Picard and, in contemporary terminology, establish the unirationality of varieties of connected complex groups. The rationality problem for group varieties was clearly stated by C. Chevalley [1] as late as 1954. Progress in this direction is closely connected with achievements in the structure theory of algebraic groups. Thus, the Levi decomposition enables one to reduce the rationality problem to the case of reductive groups, and the Bruhat decomposition is the key to proving the rationality of varieties of reductive groups over any algebraically
 |
closed field (cf. Reductive group). Thus, in the geometrical case definitive results have been obtained.
The situation for algebraically non-closed fields  turns out to be much more complicated. Examples of non-rational
turns out to be much more complicated. Examples of non-rational  -varieties are supplied by algebraic tori; for example, a three-dimensional torus
-varieties are supplied by algebraic tori; for example, a three-dimensional torus  , corresponding to the biquadratic extension
, corresponding to the biquadratic extension 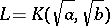 of
of  (see [1]). This example is minimal, for tori of dimension
(see [1]). This example is minimal, for tori of dimension  are rational. Algebraic tori are always unirational. Arbitrary connected
are rational. Algebraic tori are always unirational. Arbitrary connected 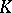 -groups are not necessarily unirational [3], but if
-groups are not necessarily unirational [3], but if 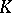 is perfect or
is perfect or 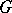 is reductive, unirationality can be proved (see [1]–[4]). Thus, the rationality problem for group varieties has the character of the Lüroth problem over an algebraically non-closed field.
is reductive, unirationality can be proved (see [1]–[4]). Thus, the rationality problem for group varieties has the character of the Lüroth problem over an algebraically non-closed field.
Since an arbitrary reductive group is the almost-direct product of a torus and a semi-simple group, one can naturally distinguish two main cases: 1)  is a torus; or 2)
is a torus; or 2) 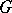 is a semi-simple group. The first case is investigated using various cohomological invariants (for semi-simple groups, these invariants turn out to be ineffective). Fairly complete results are obtained for tori which split over an Abelian extension of the ground field (see [5]). The first example of a non-rational variety in the class of semi-simple groups was a non-simply-connected group, whose construction is actually contained in [10]. The resulting conjecture, that varieties of simply-connected groups are always rational, was solved negatively by V.P. Platonov, using reduced
is a semi-simple group. The first case is investigated using various cohomological invariants (for semi-simple groups, these invariants turn out to be ineffective). Fairly complete results are obtained for tori which split over an Abelian extension of the ground field (see [5]). The first example of a non-rational variety in the class of semi-simple groups was a non-simply-connected group, whose construction is actually contained in [10]. The resulting conjecture, that varieties of simply-connected groups are always rational, was solved negatively by V.P. Platonov, using reduced 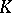 -theory (see [6], [7]). It was found that the reduced Whitehead group
-theory (see [6], [7]). It was found that the reduced Whitehead group 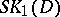 of a finite-dimensional central simple
of a finite-dimensional central simple  -algebra
-algebra 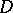 is trivial if the variety determined by
is trivial if the variety determined by 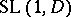 is rational over
is rational over 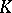 . These results carry over to unitary groups [12]. There are results on the rationality of the spinor varieties
. These results carry over to unitary groups [12]. There are results on the rationality of the spinor varieties 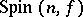 , where
, where  is a non-degenerate quadratic form in
is a non-degenerate quadratic form in  variables over
variables over 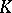 (
(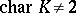 ). Spinor varieties are rational if either
). Spinor varieties are rational if either  , or
, or 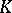 is locally compact and non-discrete, or is the field of rational numbers (see [8], [9], [11]); for
is locally compact and non-discrete, or is the field of rational numbers (see [8], [9], [11]); for 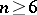 there are spinor varieties that are not rational [8]. The last result is astonishing, in that
there are spinor varieties that are not rational [8]. The last result is astonishing, in that  is a two-sheeted covering of the rational variety
is a two-sheeted covering of the rational variety 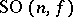 .
.
The term "rationality theorem" is sometimes used in the theory of algebraic groups in a somewhat different sense, in connection with assertions about the properties of groups over a, not necessarily algebraically closed, field, such as the Rosenlicht–Grothendieck theorem, which states that any connected 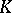 -group possesses a maximal torus defined over
-group possesses a maximal torus defined over 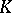 (see [4]).
(see [4]).
References
| [1] | C. Chevalley, "On algebraic group varieties" J. Math. Soc. Japan , 6 : 3/4 (1954) pp. 303–324 |
| [2] | M. Demazure, A. Grothendieck, "Schemas en groupes II" , Lect. notes in math. , 152 , Springer (1970) |
| [3] | M. Rosenlicht, "Some rationality questions on algebraic groups" Ann. Mat. Pura Appl. , 43 (1957) pp. 25–50 |
| [4] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [5] | V.E. Voskresenskii, "Algebraic tori" , Moscow (1977) (In Russian) |
| [6] | V.P. Platonov, "Reduced 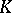 -theory and approximation in algebraic groups" Proc. Steklov Inst. Math. , 142 (1976) pp. 213–224 Trudy Mat. Inst. Steklov. , 142 (1976) pp. 198–207 -theory and approximation in algebraic groups" Proc. Steklov Inst. Math. , 142 (1976) pp. 213–224 Trudy Mat. Inst. Steklov. , 142 (1976) pp. 198–207 |
| [7] | V.P. Platonov, "Birational properties of the reduced Whitehead group" Dokl. Akad. Nauk BSSR , 21 : 3 (1977) pp. 197–198 (In Russian) |
| [8] | V.P. Platonov, "On the problem of rationality of spinor varieties" Soviet Math. Dokl. , 20 : 5 (1979) pp. 1027–1031 Dokl. Akad. Nauk SSSR , 248 : 3 (1979) pp. 524–527 |
| [9] | V.P. Platonov, "Birational properties of spinor varieties" Proc. Steklov Inst. Math. , 157 (1981) pp. 173–182 Trudy Mat. Inst. Steklov. , 157 (1981) pp. 161–169 |
| [10] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [11] | V.I. Chernousov, "On the rationality of spinor varieties over the rational number field" Dokl. Akad. Nauk BSSR , 25 : 4 (1981) pp. 293–296 (In Russian) (English abstract) |
| [12] | V.I. Yanchevskii, "Reduced  -theory. Applications to algebraic groups" Math. USSR Sb. , 38 : 4 (1981) pp. 533–548 Mat. Sb. , 110 : 4 (1979) pp. 579–596 -theory. Applications to algebraic groups" Math. USSR Sb. , 38 : 4 (1981) pp. 533–548 Mat. Sb. , 110 : 4 (1979) pp. 579–596 |
Comments
Unirationality results imply density results for rational points. For example, if 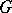 is a connected reductive group over an infinite field
is a connected reductive group over an infinite field 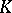 , the group
, the group 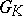 of
of 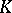 -rational points is Zariski-dense in
-rational points is Zariski-dense in  .
.
The Rosenlicht–Grothendieck theorem is often simply called the Grothendieck theorem.
Rationality theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rationality_theorems&oldid=18791