Difference between revisions of "Rational tangles"
From Encyclopedia of Mathematics
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 10 formulas out of 12 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 12 formulas, 10 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A family of $2$-tangles (cf. [[Tangle|Tangle]]) classified by J.H. Conway. The $2$-tangle of Fig.a1 is called a rational tangle with Conway notation $T ( a _ { 1 } , \dots , a _ { n } )$. It is a rational $p / q$-tangle if | ||
| − | <img | + | \begin{equation*} \frac { p } { q } = a _ { n } + \frac { 1 } { a _ { n - 1} + \ldots + \frac { 1 } { a_ { 1 } } }. \end{equation*} |
| + | |||
| + | The fraction $p / q$ is called the slope of the tangle and can be identified with the slope of the meridian disc of the solid torus that is the branched double covering of the rational tangle. | ||
| + | |||
| + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/r130030a.gif" style="border:1px solid;"/> | ||
Figure: r130030a | Figure: r130030a | ||
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/r130030b.gif" style="border:1px solid;"/> |
Figure: r130030b | Figure: r130030b | ||
| − | Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational | + | Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational $n$-tangle (also called an $n$-bridge $n$-tangle) is an $n$-tangle that can be obtained from the identity tangle by a finite number of additions of a single crossing. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J.H. Conway, "An enumeration of knots and links" J. Leech (ed.) , ''Computational Problems in Abstract Algebra'' , Pergamon Press (1969) pp. 329–358</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Kawauchi, "A survey of knot theory" , Birkhäuser (1996)</td></tr></table> |
Revision as of 15:30, 1 July 2020
A family of $2$-tangles (cf. Tangle) classified by J.H. Conway. The $2$-tangle of Fig.a1 is called a rational tangle with Conway notation $T ( a _ { 1 } , \dots , a _ { n } )$. It is a rational $p / q$-tangle if
\begin{equation*} \frac { p } { q } = a _ { n } + \frac { 1 } { a _ { n - 1} + \ldots + \frac { 1 } { a_ { 1 } } }. \end{equation*}
The fraction $p / q$ is called the slope of the tangle and can be identified with the slope of the meridian disc of the solid torus that is the branched double covering of the rational tangle.
Figure: r130030a
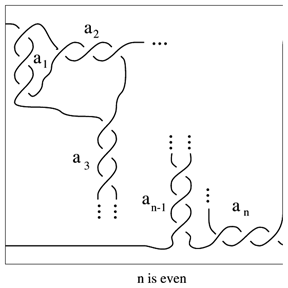
Figure: r130030b
Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational $n$-tangle (also called an $n$-bridge $n$-tangle) is an $n$-tangle that can be obtained from the identity tangle by a finite number of additions of a single crossing.
References
| [a1] | J.H. Conway, "An enumeration of knots and links" J. Leech (ed.) , Computational Problems in Abstract Algebra , Pergamon Press (1969) pp. 329–358 |
| [a2] | A. Kawauchi, "A survey of knot theory" , Birkhäuser (1996) |
How to Cite This Entry:
Rational tangles. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_tangles&oldid=13459
Rational tangles. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_tangles&oldid=13459
This article was adapted from an original article by Jozef Przytycki (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article