Rational surface
A two-dimensional algebraic variety, defined over an algebraically closed field  , whose field of rational functions is a purely transcendental extension of
, whose field of rational functions is a purely transcendental extension of 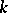 of degree 2. Every rational surface
of degree 2. Every rational surface 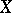 is birationally isomorphic to the projective space
is birationally isomorphic to the projective space 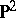 .
.
The geometric genus  and the irregularity
and the irregularity  of a complete smooth rational surface
of a complete smooth rational surface  are equal to 0, that is, there are no regular differential 2- or
are equal to 0, that is, there are no regular differential 2- or 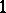 -forms on
-forms on 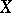 . Every multiple genus
. Every multiple genus  of a smooth complete rational surface
of a smooth complete rational surface 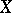 is also zero, where
is also zero, where 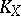 is the canonical divisor of the surface
is the canonical divisor of the surface 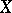 . These birational invariants distinguish the rational surfaces among all algebraic surfaces, that is, any smooth complete algebraic surface with invariants
. These birational invariants distinguish the rational surfaces among all algebraic surfaces, that is, any smooth complete algebraic surface with invariants 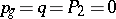 is a rational surface (the Castelnuovo rationality criterion). According to another rationality criterion, a smooth algebraic surface
is a rational surface (the Castelnuovo rationality criterion). According to another rationality criterion, a smooth algebraic surface  is a rational surface if and only if there is a non-singular rational curve
is a rational surface if and only if there is a non-singular rational curve 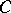 on
on 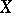 with index of self-intersection
with index of self-intersection 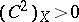 .
.
With the exception of rational surfaces and ruled surfaces, every algebraic surface is birationally isomorphic to a unique minimal model. In the class of rational surfaces there is a countable set of minimal models. It consists of the projective space 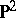 and the surfaces
and the surfaces 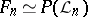 (projectivization of two-dimensional vector bundles over the projective line
(projectivization of two-dimensional vector bundles over the projective line 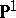 ),
), 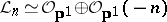 , where
, where 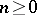 and
and 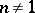 . In other words, the surface
. In other words, the surface 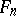 is a fibration by rational curves over a rational curve with a section
is a fibration by rational curves over a rational curve with a section 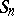 which is a smooth rational curve with index of self-intersection
which is a smooth rational curve with index of self-intersection  . The surface
. The surface 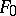 is isomorphic to the direct product
is isomorphic to the direct product 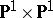 , and the surfaces
, and the surfaces 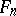 are obtained from
are obtained from 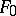 by a sequence of elementary transformations (see [1]).
by a sequence of elementary transformations (see [1]).
Rational surfaces have a large group of birational transformations (called the group of Cremona transformations).
If the anti-canonical sheaf 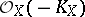 on a smooth complete rational surface is ample (cf. Ample sheaf), then
on a smooth complete rational surface is ample (cf. Ample sheaf), then 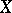 is called a Del Pezzo surface. The greatest integer
is called a Del Pezzo surface. The greatest integer 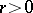 such that
such that 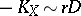 for some divisor
for some divisor 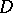 on
on  is called the index of the Del Pezzo surface. The index
is called the index of the Del Pezzo surface. The index  is equal to 1, 2 or 3 (see [2]). A Del Pezzo surface of index 3 is isomorphic to
is equal to 1, 2 or 3 (see [2]). A Del Pezzo surface of index 3 is isomorphic to 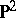 . For a Del Pezzo surface
. For a Del Pezzo surface 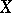 of index 2, the rational mapping
of index 2, the rational mapping 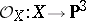 defined by the sheaf
defined by the sheaf 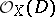 gives a birational isomorphism onto a quadric in
gives a birational isomorphism onto a quadric in 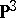 . Del Pezzo surfaces of index 1 can be obtained by
. Del Pezzo surfaces of index 1 can be obtained by  monoidal transformations (cf. Monoidal transformation) of the plane
monoidal transformations (cf. Monoidal transformation) of the plane 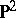 with centres at points in general position, where
with centres at points in general position, where 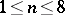 (see [2]).
(see [2]).
References
| [1] | I.R. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) |
| [2] | V.A. Iskovskii, "Anticanonical models of three-dimensional algebraic varieties" , Current problems in mathematics , 12 , Moscow (1979) pp. 59–157; 239 (In Russian) |
| [3] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Comments
If 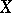 is defined over a, not necessarily algebraically closed, field and
is defined over a, not necessarily algebraically closed, field and 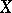 is birationally equivalent to
is birationally equivalent to 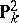 over
over 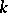 , then
, then 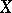 is said to be a
is said to be a 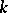 -rational surface.
-rational surface.
References
| [a1] | A. Beauville, "Surfaces algébriques complexes" Astérisque , 54 (1978) |
| [a2] | J. Semple, L. Roth, "Introduction to algebraic geometry" , Oxford Univ. Press (1985) |
Rational surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_surface&oldid=11514