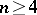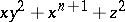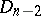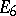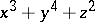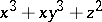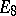Rational singularity
A normal singular point 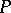 of an algebraic variety or complex-analytic space
of an algebraic variety or complex-analytic space 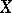 admitting a resolution
admitting a resolution 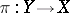 (cf. Resolution of singularities), under which the direct images
(cf. Resolution of singularities), under which the direct images 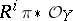 of the structure sheaf
of the structure sheaf 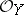 are trivial for
are trivial for 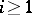 . Then any resolution of the given singularity will have this property. If the ground field has characteristic 0, then a singularity is rational if and only if
. Then any resolution of the given singularity will have this property. If the ground field has characteristic 0, then a singularity is rational if and only if 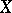 is a Cohen–Macaulay variety and the imbedding
is a Cohen–Macaulay variety and the imbedding 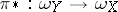 of dual sheaves is an isomorphism [5].
of dual sheaves is an isomorphism [5].
Some examples of rational singularities are the singular points of the quotient space 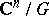 , where
, where 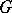 is a finite group of linear transformations, the singular point 0 of the hypersurface
is a finite group of linear transformations, the singular point 0 of the hypersurface 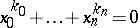 when
when  (see [8]), and toric singularities.
(see [8]), and toric singularities.
If  is a Gorenstein isolated singularity (i.e. the sheaf
is a Gorenstein isolated singularity (i.e. the sheaf 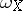 is locally free) over the field
is locally free) over the field  and
and 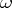 is a generating section of
is a generating section of 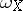 , then
, then  is a rational singularity if and only if
is a rational singularity if and only if
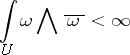 |
in a sufficiently small neighbourhood  of the point (see [7]).
of the point (see [7]).
In the case when  , a singularity
, a singularity  is rational if and only if
is rational if and only if  for every cycle
for every cycle 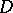 on the exceptional curve
on the exceptional curve 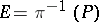 of the resolution
of the resolution 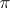 . In this case, all the components
. In this case, all the components 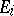 of
of 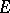 are isomorphic to the projective line
are isomorphic to the projective line 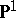 ,
, 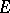 is a divisor with normal intersections and the graph
is a divisor with normal intersections and the graph 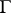 of the resolution is a tree.
of the resolution is a tree.
The fundamental cycle of a singularity is defined as the minimal cycle 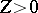 on
on  for which
for which 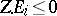 for all
for all 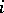 . There is a criterion of rationality in terms of
. There is a criterion of rationality in terms of 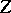 :
: 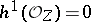 , and one can calculate the multiplicity of the singularity and the dimension of the tangent space [1].'
, and one can calculate the multiplicity of the singularity and the dimension of the tangent space [1].'
<tbody> </tbody>
|
Rational singularities of hypersurfaces 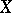 in a three-dimensional affine space
in a three-dimensional affine space 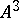 , equivalently, two-dimensional rational singularities of multiplicity 2, are called rational double points. Rational double points admit various equivalent characterizations and have various names, such as Klein singularities, Du Val singularities and simple singularities. The equations of rational double points arose as equations relating invariants of symmetry groups of regular polyhedra (see [6]). To this corresponds a characterization of rational double points as singularities of the quotient space
, equivalently, two-dimensional rational singularities of multiplicity 2, are called rational double points. Rational double points admit various equivalent characterizations and have various names, such as Klein singularities, Du Val singularities and simple singularities. The equations of rational double points arose as equations relating invariants of symmetry groups of regular polyhedra (see [6]). To this corresponds a characterization of rational double points as singularities of the quotient space 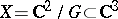 , where
, where 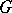 is a finite subgroup of
is a finite subgroup of 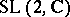 ; that is, up to conjugacy,
; that is, up to conjugacy, 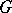 is either the cyclic group
is either the cyclic group  or order
or order  , the binary dihedral group
, the binary dihedral group  , the tetrahedral group
, the tetrahedral group 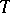 , the octahedral group
, the octahedral group 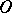 , or the icosahedral group
, or the icosahedral group 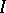 . If
. If 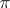 is a minimal resolution of a rational double point, then
is a minimal resolution of a rational double point, then 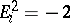 for all
for all 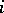 , and the weighted (resolution) graph
, and the weighted (resolution) graph 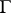 coincides with the diagram of simple roots of one of the semi-simple Lie algebras
coincides with the diagram of simple roots of one of the semi-simple Lie algebras 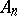 ,
,  ,
,  ,
, 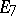 , or
, or 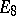 , whose symbol is also used to denote the singularity (cf. Lie algebra, semi-simple). Such a singularity is determined up to an isomorphism by its weighted graph
, whose symbol is also used to denote the singularity (cf. Lie algebra, semi-simple). Such a singularity is determined up to an isomorphism by its weighted graph 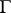 ([3], [11]), as depicted in the table above. Rational double points can be characterized as two-dimensional Gorenstein rational singularities. They are also called canonical singularities, since they are just those singularities which appear in canonical models of algebraic surfaces of general type.
([3], [11]), as depicted in the table above. Rational double points can be characterized as two-dimensional Gorenstein rational singularities. They are also called canonical singularities, since they are just those singularities which appear in canonical models of algebraic surfaces of general type.
If 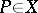 is a Gorenstein rational singularity of arbitrary dimension, then its general hypersurface section is either a rational or an elliptic Gorenstein singularity, and this leads, in particular, to a characterization of three-dimensional rational singularities (see [8]).
is a Gorenstein rational singularity of arbitrary dimension, then its general hypersurface section is either a rational or an elliptic Gorenstein singularity, and this leads, in particular, to a characterization of three-dimensional rational singularities (see [8]).
The following assertions are true in all dimensions (see [4]).
1) A deformation of a rational singularity is again a rational singularity.
2) If  is a flat morphism and
is a flat morphism and 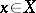 is such that
is such that 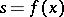 is a rational singularity in
is a rational singularity in  and
and  is a rational singularity of the fibre
is a rational singularity of the fibre 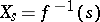 , then
, then  is a rational singularity in
is a rational singularity in 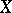 .
.
3) If a deformation 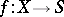 has a smooth base
has a smooth base 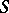 and admits a simultaneous resolution of singularities, then a point
and admits a simultaneous resolution of singularities, then a point 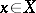 is a rational singularity if and only if
is a rational singularity if and only if  is a rational singularity in its own fibre
is a rational singularity in its own fibre 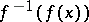 .
.
In the case when 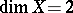 , every deformation of a variety
, every deformation of a variety  resolving a rational singularity
resolving a rational singularity 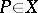 defines a deformation of
defines a deformation of 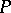 , obtained by contracting the exceptional curves of the fibres of the given deformation. As a result, one obtains a morphism
, obtained by contracting the exceptional curves of the fibres of the given deformation. As a result, one obtains a morphism 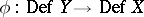 of the bases of versal deformations of the variety
of the bases of versal deformations of the variety 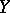 and the singularity
and the singularity 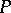 . The image
. The image 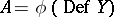 is a non-singular irreducible component of
is a non-singular irreducible component of 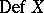 , called the Artin component, and
, called the Artin component, and 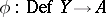 is a Galois covering whose group
is a Galois covering whose group 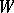 can be found using the graph
can be found using the graph 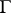 of the singularity
of the singularity 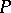 (see [2], [10]). In particular, for a double rational singularity
(see [2], [10]). In particular, for a double rational singularity 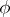 is surjective and
is surjective and  coincides with the Weyl group of the corresponding Lie algebra, that is, a versal deformation of a rational singularity is simultaneously resolved after the Galois covering of the base of the deformation with Weyl group
coincides with the Weyl group of the corresponding Lie algebra, that is, a versal deformation of a rational singularity is simultaneously resolved after the Galois covering of the base of the deformation with Weyl group  (see [9]).
(see [9]).
References
| [1] | M. Artin, "On isolated rational singularities of surfaces" Amer. J. Math. , 88 (1966) pp. 129–136 |
| [2] | M. Artin, "Algebraic construction of Brieskorn's resolutions" J. Algebra , 29 : 2 (1974) pp. 330–348 |
| [3] | E. Brieskorn, "Rationale singularitäten komplexer Flächen" Invent. Math. , 4 (1968) pp. 336–358 |
| [4] | R. Elkik, "Singularités rationelles et déformations" Invent. Math. , 47 (1978) pp. 139–147 |
| [5] | G. Kempf, "Cohomology and convexity" G. Kempf (ed.) et al. (ed.) , Toroidal embeddings , Lect. notes in math. , 339 , Springer (1973) pp. 41–52 |
| [6] | F. Klein, "Lectures on the icosahedron and the solution of equations of the fifth degree" , Dover, reprint (1956) (Translated from German) |
| [7] | H.B. Laufer, "On rational singularities" Amer. J. Math. , 94 (1972) pp. 597–608 |
| [8] | M. Reid, "Canonical 3-folds" J. Geom. Alg. Angers (1980) pp. 273–310 |
| [9] | P.J. Slodowy, "Simple singularities and simple algebraic groups" , Lect. notes in math. , 815 , Springer (1980) |
| [10] | J.M. Wahl, "Simultaneous resolution of rational singularities" Compos. Math. , 38 (1979) pp. 43–54 |
| [11] | G.N. Tyurina, "On the tautness of rationally contractible curves on a surface" Math. USSR Izv. , 2 (1968) pp. 907–934 Izv. Akad. Nauk SSSR. Ser. Mat. , 32 (1968) pp. 943–970 |
Comments
See also Dynkin diagram.
References
| [a1] | M. Demazure (ed.) H. Pinkham (ed.) B. Teissier (ed.) , Sem. singularités des surfaces , Lect. notes in math. , 777 , Springer (1980) |
| [a2] | A. Durfee, "Fifteen characterizations of rational double points and simple critical points" Ens. Math. , 25 (1979) pp. 131–163 |
Rational singularity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_singularity&oldid=19123

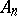 ,
, 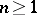
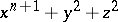
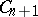
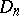 ,
,