Rank of an algebraic group
The dimension of a Cartan subgroup of it (this dimension does not depend on the choice of the Cartan subgroup). Along with the rank of an algebraic group 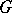 one considers its semi-simple rank and reductive rank, which, by definition, are equal to the rank of the algebraic group
one considers its semi-simple rank and reductive rank, which, by definition, are equal to the rank of the algebraic group 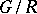 and the rank of the algebraic group
and the rank of the algebraic group 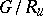 respectively, where
respectively, where 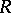 is the radical of the algebraic group
is the radical of the algebraic group 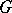 and
and 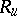 is its unipotent radical (cf. Radical of a group; Unipotent element). The reductive rank of an algebraic group
is its unipotent radical (cf. Radical of a group; Unipotent element). The reductive rank of an algebraic group 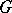 is equal to the dimension of any of its maximal tori (cf. Maximal torus). The reductive
is equal to the dimension of any of its maximal tori (cf. Maximal torus). The reductive 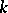 -rank of a linear algebraic group
-rank of a linear algebraic group 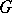 defined over a field
defined over a field 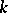 (and in the case when the group
(and in the case when the group 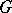 is reductive (cf. Reductive group) — simply its
is reductive (cf. Reductive group) — simply its 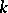 -rank) is the dimension of a maximal
-rank) is the dimension of a maximal 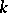 -split torus of it (this dimension does not depend on the choice of a torus; see Split group). If the
-split torus of it (this dimension does not depend on the choice of a torus; see Split group). If the 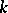 -rank of a reductive linear algebraic group
-rank of a reductive linear algebraic group 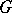 over
over 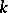 is zero (is equal to the rank of
is zero (is equal to the rank of 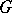 ), then the group
), then the group 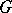 is said to be anisotropic (or split, respectively) over
is said to be anisotropic (or split, respectively) over 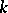 (see also Anisotropic group).
(see also Anisotropic group).
Examples.
1) The rank of the algebraic group 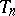 of all non-singular upper-triangular square matrices of order
of all non-singular upper-triangular square matrices of order  is equal to its reductive rank and equal to
is equal to its reductive rank and equal to  ; the semi-simple rank of
; the semi-simple rank of 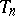 is zero.
is zero.
2) The rank of the algebraic group 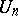 of all upper-triangular square matrices of order
of all upper-triangular square matrices of order  with 1 on the principal diagonal is equal to its dimension
with 1 on the principal diagonal is equal to its dimension 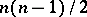 , and the reductive and semi-simple ranks of
, and the reductive and semi-simple ranks of 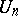 are zero.
are zero.
3) The rank of the algebraic group 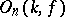 of all
of all 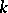 -automorphisms of a definite quadratic form
-automorphisms of a definite quadratic form 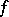 on an
on an  -dimensional vector space over a field
-dimensional vector space over a field 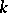 is equal to
is equal to 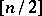 , and the
, and the 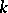 -rank of the group
-rank of the group 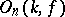 is equal to the Witt index of the form
is equal to the Witt index of the form  .
.
If the characteristic of the ground field is 0, then the rank of the algebraic group  coincides with the rank of its Lie algebra
coincides with the rank of its Lie algebra 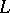 (see Rank of a Lie algebra) and is equal to the minimum multiplicity of the eigen value
(see Rank of a Lie algebra) and is equal to the minimum multiplicity of the eigen value 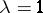 of all possible adjoint operators
of all possible adjoint operators 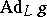 (the minimum is taken over all
(the minimum is taken over all 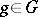 ). An element
). An element 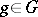 for which this multiplicity is equal to the rank of the algebraic group
for which this multiplicity is equal to the rank of the algebraic group  is called regular. The set of regular elements of
is called regular. The set of regular elements of 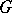 is open in the Zariski topology on
is open in the Zariski topology on  .
.
References
| [1] | C. Chevalley, "Théorie des groupes de Lie" , 2–3 , Hermann (1952–1955) |
| [2] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–250 |
| [3] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [4] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
Rank of an algebraic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_of_an_algebraic_group&oldid=16419