Random walk
A stochastic process of special form that can be interpreted as a model describing the movement of a particle in a certain state space under the action of some random mechanism. The state space is usually a 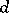 -dimensional Euclidean space or the integral lattice in it. The random mechanism can be of various kinds; the most common random walks are those generated by summation of independent random variables or by Markov chains. There is no precise generally-accepted definition of a random walk.
-dimensional Euclidean space or the integral lattice in it. The random mechanism can be of various kinds; the most common random walks are those generated by summation of independent random variables or by Markov chains. There is no precise generally-accepted definition of a random walk.
The trajectories of the simplest random walk in the case 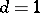 are described by the initial position
are described by the initial position  and the sequence of sums
and the sequence of sums
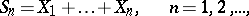 | (1) |
where the 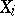 are independent and have a Bernoulli distribution:
are independent and have a Bernoulli distribution:
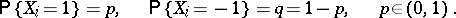 |
The value of 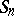 can be interpreted as the gain of one of two players after
can be interpreted as the gain of one of two players after  games in each of which this player wins one dollar with probability
games in each of which this player wins one dollar with probability 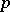 and loses it with probability
and loses it with probability 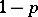 . If the game consists of tossing an unbiased coin, then it is assumed that
. If the game consists of tossing an unbiased coin, then it is assumed that 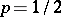 (a symmetric walk, see Bernoulli random walk). Under the assumption that the initial capital of the first player is
(a symmetric walk, see Bernoulli random walk). Under the assumption that the initial capital of the first player is 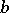 and that of the second player is
and that of the second player is  , the game will finish when the moving particle (with coordinates
, the game will finish when the moving particle (with coordinates 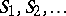 ) first touches one of the levels
) first touches one of the levels  or
or 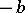 . At this moment, one of the players is ruined. This is the classical ruin problem, in which the boundaries at points
. At this moment, one of the players is ruined. This is the classical ruin problem, in which the boundaries at points  and
and 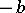 can be regarded as absorbing.
can be regarded as absorbing.
In applications to queueing theory, the behaviour of the particle near the boundaries  and
and 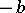 can differ: e.g., if
can differ: e.g., if 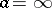 and
and 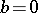 , then the position
, then the position 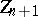 of the random particle at the moment
of the random particle at the moment 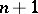 is given by
is given by
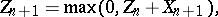 | (2) |
and the boundary at  can be called detaining or reflecting. There are also other possibilities for the behaviour of the particle in a neighbourhood of the boundaries.
can be called detaining or reflecting. There are also other possibilities for the behaviour of the particle in a neighbourhood of the boundaries.
If 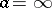 , then one obtains the problem of a random walk with one boundary. If
, then one obtains the problem of a random walk with one boundary. If 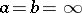 , then one obtains an unrestricted random walk. Random walks are usually studied using the apparatus of discrete Markov chains and, in particular, by investigating the corresponding finite-difference equations. For example, in the ruin problem, let
, then one obtains an unrestricted random walk. Random walks are usually studied using the apparatus of discrete Markov chains and, in particular, by investigating the corresponding finite-difference equations. For example, in the ruin problem, let 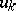 be the probability that the first player is ruined, given that his initial capital is equal to
be the probability that the first player is ruined, given that his initial capital is equal to 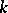 ,
, 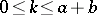 , where the total capital of both players is fixed and equal to
, where the total capital of both players is fixed and equal to 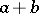 . Then, by the total probability formula (at the first jump), it follows that
. Then, by the total probability formula (at the first jump), it follows that 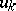 satisfies the equation
satisfies the equation
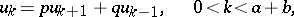 |
and the boundary conditions 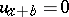 ,
,  . Thus one obtains
. Thus one obtains
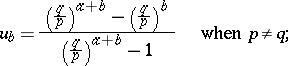 |
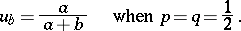 |
The second of these formulas shows that even a "fair" game (in which both players have identical chances) leads to ruin with probability close to 1, provided that the capital  of the second player is large in comparison to
of the second player is large in comparison to 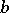 (
( when
when 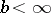 ,
, 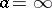 ).
).
The ruin problem has been thoroughly investigated. For example, it was shown by J. Lagrange (see [1], Vol. 1) that the probability 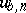 of ruin of the first player at the
of ruin of the first player at the  -th step, given that this initial capital is
-th step, given that this initial capital is 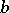 , where the total capital is
, where the total capital is 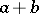 (fixed), is equal to
(fixed), is equal to
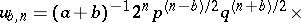 |
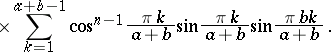 |
The mean time before ruin of one of the players, 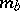 , is given by
, is given by
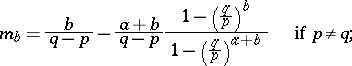 |
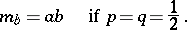 |
For random walks with one boundary  , described by (2), there is a stationary distribution for the random walk when
, described by (2), there is a stationary distribution for the random walk when 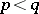 and
and 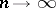 , coinciding with the distribution of the random variable
, coinciding with the distribution of the random variable 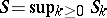 and
and
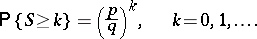 | (3) |
The laws describing an unrestricted random walk follow from theorems about the behaviour of the sequence of partial sums 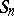 ,
, 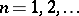 . One of these laws confirms that for a symmetric random walk
. One of these laws confirms that for a symmetric random walk 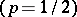 , the particle hits (infinitely often) any fixed point
, the particle hits (infinitely often) any fixed point  with probability 1. When
with probability 1. When 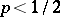 , the walk departs to the left with probability 1; in this case
, the walk departs to the left with probability 1; in this case 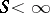 with probability 1.
with probability 1.
For a symmetric random walk, the time 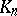 spent by the particle on the positive half-line (the number of positive terms in the sequence
spent by the particle on the positive half-line (the number of positive terms in the sequence 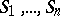 ) will be closer to
) will be closer to  or
or  than to
than to 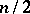 with a large probability. This is seen from the so-called arcsine law, which implies that for large
with a large probability. This is seen from the so-called arcsine law, which implies that for large  (see [1], Vol. 1),
(see [1], Vol. 1),
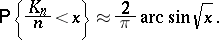 |
This implies, for example, that
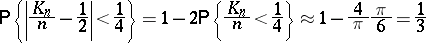 |
and that with probability 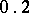 , the particle spends at least
, the particle spends at least 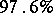 of the whole time on one side.
of the whole time on one side.
There are relations connecting random walks with boundaries with unrestricted random walks. For example, if one assumes that 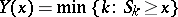 , then (see [2])
, then (see [2])
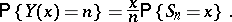 |
In an unrestricted random walk, the position 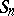 of the particle for large
of the particle for large  is described by the law of large numbers and the central limit theorem.
is described by the law of large numbers and the central limit theorem.
If the magnitudes 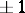 of the jumps are changed to
of the jumps are changed to 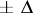 (for small
(for small 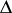 ) and if one assumes that
) and if one assumes that 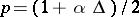 , then the position
, then the position 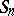 of the particle after
of the particle after 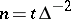 steps will describe approximately (as
steps will describe approximately (as  ) the behaviour at time
) the behaviour at time 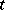 of the diffusion process with drift
of the diffusion process with drift 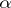 , diffusion coefficient 1, and corresponding behaviour on the boundaries
, diffusion coefficient 1, and corresponding behaviour on the boundaries  and
and 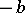 (if these are specified for the random walk
(if these are specified for the random walk 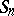 ).
).
The notion of a random walk as described above can be generalized in many ways. The simplest random walks in 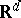 for
for 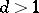 are defined as follows. The particle leaves the origin and moves one step of length 1 in one of the
are defined as follows. The particle leaves the origin and moves one step of length 1 in one of the 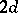 directions parallel to the coordinate axes. Thus, its possible positions are the points of
directions parallel to the coordinate axes. Thus, its possible positions are the points of 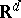 with integer coordinates. To define a random walk it is necessary to specify
with integer coordinates. To define a random walk it is necessary to specify 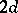 probabilities corresponding to the different directions. One obtains a symmetric random walk if all these are equal to
probabilities corresponding to the different directions. One obtains a symmetric random walk if all these are equal to 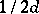 . In the multi-dimensional case, the problem of a random walk with boundaries becomes much more complicated, since the shape of the boundaries becomes essentially more complex when
. In the multi-dimensional case, the problem of a random walk with boundaries becomes much more complicated, since the shape of the boundaries becomes essentially more complex when 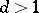 . In the unrestricted case, Pólya's theorem holds (see [1], Vol. 1): for a symmetric random walk when
. In the unrestricted case, Pólya's theorem holds (see [1], Vol. 1): for a symmetric random walk when 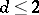 , the particle will sooner or later return to its initial position with probability 1 (once, and thus infinitely often); but when
, the particle will sooner or later return to its initial position with probability 1 (once, and thus infinitely often); but when 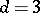 this probability is approximately equal to 0.35 (and when
this probability is approximately equal to 0.35 (and when 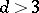 it is still smaller).
it is still smaller).
Another possible generalization of the simplest random walk consists of taking arbitrarily distributed independent random variables 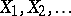 in (1). In this case, the basic qualitative laws for unrestricted random walks and for random walks with boundaries are preserved. For example, the particle reaches one of the boundaries
in (1). In this case, the basic qualitative laws for unrestricted random walks and for random walks with boundaries are preserved. For example, the particle reaches one of the boundaries  or
or 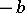 with probability 1. If
with probability 1. If 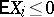 and
and 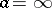 , then the boundary
, then the boundary 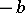 will be reached with probability 1. If the
will be reached with probability 1. If the 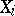 are integer valued and
are integer valued and 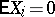 , then the particle will return to the initial position with probability 1. For arbitrarily distributed
, then the particle will return to the initial position with probability 1. For arbitrarily distributed 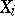 with
with 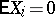 , this statement only holds in case one considers return to an interval, not to a point.
, this statement only holds in case one considers return to an interval, not to a point.
The solution of problems concerned with the exit of random walks from an interval 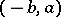 turns out to be much more difficult in the general case. At the same time, these problems have many applications in mathematical statistics (sequential analysis), in the insurance business, in queueing theory, etc. In their investigation, a decisive role is played by various functionals of a random walk
turns out to be much more difficult in the general case. At the same time, these problems have many applications in mathematical statistics (sequential analysis), in the insurance business, in queueing theory, etc. In their investigation, a decisive role is played by various functionals of a random walk 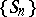 ,
, 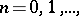 called boundary functionals. Among these are
called boundary functionals. Among these are 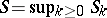 , the time of the first passage through zero (in a positive direction),
, the time of the first passage through zero (in a positive direction), 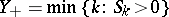 , the time of the first passage through zero (in a negative direction),
, the time of the first passage through zero (in a negative direction), 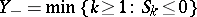 , the first positive sum
, the first positive sum 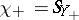 , and the first non-positive sum
, and the first non-positive sum 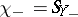 , etc. It turns out that the distribution of the jumps
, etc. It turns out that the distribution of the jumps 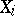 is connected with the distribution of these functionals by the following so-called factorization identity (see [1], Vol. 1; [2], [3]; see also Factorization identities). Let
is connected with the distribution of these functionals by the following so-called factorization identity (see [1], Vol. 1; [2], [3]; see also Factorization identities). Let 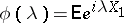 be the characteristic function of
be the characteristic function of 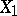 . Then, when
. Then, when 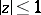 and
and 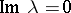 ,
,
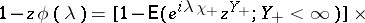 | (4) |
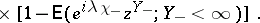 |
This identity reveals the connection between boundary problems for random walks and those in the theory of functions of a complex variable, since the factors on the right-hand side of (4) are uniquely determined by those in the canonical factorization of the function 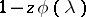 on the axis
on the axis 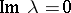 , that is, the expansion of this function as a product
, that is, the expansion of this function as a product 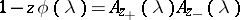 for
for 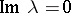 , where
, where 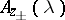 are analytic in the upper and lower half-planes, respectively, do not have zeros and are continuous there (including the boundary). In the identity (4), when
are analytic in the upper and lower half-planes, respectively, do not have zeros and are continuous there (including the boundary). In the identity (4), when 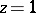 one can replace the first factor by
one can replace the first factor by
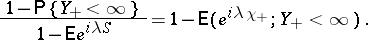 |
Identity (4) is just one of a group of factorization identities connecting the distributions of various boundary functionals. Another one is related to the Pollaczek–Spitzer identity
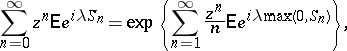 |
where 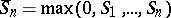 . Factorization identities provide a powerful method for studying boundary problems for random walks (see [1], Vol. 2; [2], [3]).
. Factorization identities provide a powerful method for studying boundary problems for random walks (see [1], Vol. 2; [2], [3]).
Boundary problems for random walks have been investigated rather completely, including their asymptotic analysis (see [1], Vol. 2; [4]–).
Analytically, the solution of boundary problems leads to integro-difference equations. For example, the probability 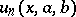 that a particle starting from a point
that a particle starting from a point 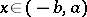 will leave this interval in time
will leave this interval in time  satisfies the following equation (the total probability formula at the first jump):
satisfies the following equation (the total probability formula at the first jump):
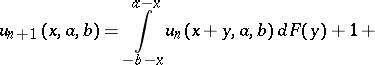 |
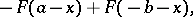 |
where 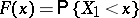 . By passing to the generating function
. By passing to the generating function 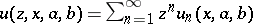 one obtains the usual integral equations. There are at least two approaches to the investigation of asymptotic properties of solutions of these equations. One of them is based on the study of analytic properties of the double transformation
one obtains the usual integral equations. There are at least two approaches to the investigation of asymptotic properties of solutions of these equations. One of them is based on the study of analytic properties of the double transformation
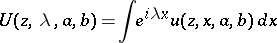 |
and its subsequent inversion (see [5]–). The other involves the methods of Vishik and Lyusternik for solving equations with a small parameter (see [4] and Differential equations with small parameter). The latter reveals profound connections between these problems and potential theory.
Much of the above carries over to the case of random walks with dependent jumps, when the random variables 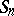 are connected in a Markov chain, and also to multi-dimensional random walks in
are connected in a Markov chain, and also to multi-dimensional random walks in 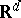 ,
, 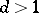 (see , [7]).
(see , [7]).
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1950–1966) |
| [2] | A.A. Borovkov, "Wahrscheinlichkeitstheorie" , Birkhäuser (1976) (Translated from Russian) |
| [3] | A.A. Borovkov, "Stochastic processes in queueing theory" , Springer (1976) (Translated from Russian) |
| [4] | V.S. Korolyuk, Yu.V. Borouvskikh, "Analytic problems in the asymptotics of probability distributions" , Kishinev (1981) (In Russian) |
| [5] | A.A. Borovkov, "New limit theorems in boundary value problems for sums of independent terms" Sibirsk. Mat. Zh. , 3 : 5 (1962) pp. 645–694 (In Russian) |
| [6a] | V.I. Lotov, "Asymptotic analysis of distributions in problems with two boundaries I" Theory Probab. Appl. , 24 (1980) pp. 480–491 Teor. Veroyatn. i Primenen. , 24 : 3 (1979) pp. 475–485 |
| [6b] | V.I. Lotov, "Asymptotic analysis of distributions in problems with two boundaries II" Theory Probab. Appl. , 24 (1980) pp. 869–876 Teor. Veroyatn. i Primenen. , 24 : 4 (1979) pp. 873–879 |
| [7] | F. Spitzer, "Principles of random walk" , v. Nostrand (1964) |
Comments
For applications to the physical and biological sciences see [a7] and the references quoted therein.
References
| [a1] | M.N. Barber, B.W. Ninham, "Random and restricted walks, theory and applications" , Gordon & Breach (1970) |
| [a2] | K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1960) |
| [a3] | A. Gut, "Stopped random walks. Limit theorems and applications" , Springer (1988) |
| [a4] | J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains" , Springer (1976) |
| [a5] | J.H.B. Kemperman, "The passage problem for a stationary Markov chain" , Univ. Chicago Press (1961) |
| [a6] | P. Lévy, "Processus stochastiques et mouvement Brownien" , Gauthier-Villars (1965) |
| [a7] | E.W. Montroll, B.J. West, "On an enriched collection of stochastic processes" E.W. Montroll (ed.) J.L. Lebowitz (ed.) , Fluctuation Phenomena , Series in Statistical Mechanics , 7 , Elsevier (1987) pp. Chapt. 2 |
| [a8] | D. Revuz, "Markov chains" , North-Holland (1975) |
Random walk. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Random_walk&oldid=16177