Radical of an ideal
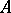 in a commutative associative ring
in a commutative associative ring 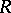
The set of all elements 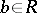 some power of which is contained in
some power of which is contained in  . This set is denoted by
. This set is denoted by 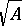 . It is an ideal in
. It is an ideal in 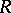 ; moreover,
; moreover, 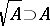 and
and 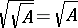 .
.
A generalization of this idea is that of the radical of a submodule. Let 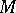 be a module over
be a module over 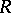 and let
and let 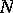 be a submodule of
be a submodule of 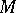 . The radical of the submodule
. The radical of the submodule 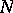 is the set of all elements
is the set of all elements 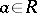 such that
such that 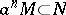 for some integer
for some integer  (in general, depending on
(in general, depending on  ). The radical of a submodule is an ideal in
). The radical of a submodule is an ideal in 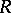 .
.
Comments
Consider the quotient ring 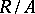 and the natural quotient homomorphism
and the natural quotient homomorphism 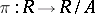 . The radical of
. The radical of 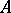 is the inverse image of the nil radical (cf. Nil ideal) of
is the inverse image of the nil radical (cf. Nil ideal) of 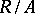 .
.
Radical ideal is the phrase sometimes used to denote an ideal that is equal to its radical.
Let 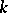 be an algebraically closed field. To each ideal
be an algebraically closed field. To each ideal 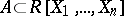 one associates the algebraic set
one associates the algebraic set 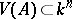 ,
, 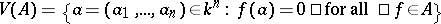 . The Hilbert Nullstellensatz says that
. The Hilbert Nullstellensatz says that 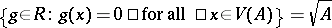 . Thus there is in this setting a bijective correspondence between radical ideals and algebraic sets.
. Thus there is in this setting a bijective correspondence between radical ideals and algebraic sets.
In the setting of affine schemes (cf. Affine scheme) 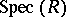 this takes the following form. To each ideal
this takes the following form. To each ideal 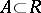 one associates the closed subspace
one associates the closed subspace 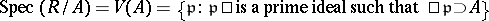 . Conversely, to each closed subspace
. Conversely, to each closed subspace 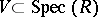 one associates the ideal
one associates the ideal 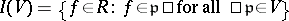 . Then again
. Then again 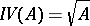 because
because 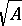 is the intersection of all prime ideals containing
is the intersection of all prime ideals containing 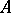 , and, again,
, and, again, 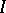 and
and  set up a bijective correspondence between radical ideals and closed subsets of
set up a bijective correspondence between radical ideals and closed subsets of 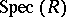 . The difference with the setting of the Nullstellensatz is that in that case only prime ideals of the form
. The difference with the setting of the Nullstellensatz is that in that case only prime ideals of the form 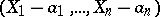 are considered.
are considered.
References
| [a1] | P.M. Cohn, "Algebra" , II , Wiley (1977) pp. Sects. 11.2, 11.10 |
| [a2] | A. Grothendieck, "Eléments de géométrie algébrique. I: Le language des schémas" Publ. Math. IHES , 20 (1960) pp. 80 |
Radical of an ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Radical_of_an_ideal&oldid=14813