Radical of a group
The largest normal subgroup of a group 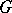 belonging to a given radical class of groups. A class of groups is called radical if it is closed under homomorphic images and also under "infinite extension" , that is, if the class contains every group having an ascending normal series with factors from the given class (see Normal series). In every group there is a largest radical normal subgroup — the radical. The quotient group by the radical is a semi-simple group, that is, it has trivial radical.
belonging to a given radical class of groups. A class of groups is called radical if it is closed under homomorphic images and also under "infinite extension" , that is, if the class contains every group having an ascending normal series with factors from the given class (see Normal series). In every group there is a largest radical normal subgroup — the radical. The quotient group by the radical is a semi-simple group, that is, it has trivial radical.
An example of a radical class is the class of groups having an ascending subnormal series with locally nilpotent factors. Sometimes the term "radical" is used just in connection with the largest locally nilpotent normal subgroup (in the case of finite groups this is the nilpotent radical or Fitting subgroup). The most important radical in finite groups is the solvable radical (see Solvable group). Finite groups having a trivial solvable radical have a description in terms of simple groups and their automorphism groups (see [1]).
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
Comments
References
| [a1] | D.J.S. Robinson, "Finiteness conditions and generalized solvable groups" , 1 , Springer (1972) pp. 20ff |
| [a2] | B.A.F. Wehrfritz, "Locally finite groups" , North-Holland (1973) pp. 12ff |
In the class of Lie groups the radical is the largest connected solvable normal subgroup. In any Lie group  there is a radical
there is a radical 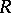 , and
, and 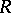 is a closed Lie subgroup in
is a closed Lie subgroup in 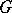 . If
. If 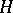 is a normal Lie subgroup in
is a normal Lie subgroup in  , then
, then 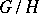 is semi-simple (see Lie group, semi-simple) if and only if
is semi-simple (see Lie group, semi-simple) if and only if 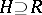 . The subalgebra of the Lie algebra
. The subalgebra of the Lie algebra 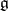 of
of 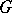 corresponding to the radical is the largest solvable ideal of the Lie algebra
corresponding to the radical is the largest solvable ideal of the Lie algebra 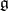 , called the radical of
, called the radical of 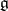 .
.
The radical of an algebraic group 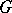 , the largest connected solvable normal subgroup of
, the largest connected solvable normal subgroup of 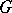 , is always closed in
, is always closed in  . The radical
. The radical 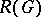 of a linear algebraic group coincides with the connected component of the identity in the intersection of all Borel subgroups (cf. Borel subgroup) of
of a linear algebraic group coincides with the connected component of the identity in the intersection of all Borel subgroups (cf. Borel subgroup) of 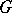 ; it is the smallest closed normal subgroup
; it is the smallest closed normal subgroup 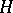 such that
such that 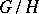 is semi-simple (see Semi-simple algebraic group). The set
is semi-simple (see Semi-simple algebraic group). The set 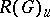 of all unipotent elements in
of all unipotent elements in 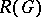 is a connected unipotent closed normal subgroup in
is a connected unipotent closed normal subgroup in 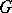 , being the largest connected unipotent closed normal subgroup. This subgroup is called the unipotent radical of
, being the largest connected unipotent closed normal subgroup. This subgroup is called the unipotent radical of 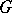 and can be characterized as the smallest closed normal subgroup
and can be characterized as the smallest closed normal subgroup 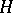 in
in 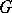 such that
such that 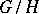 is reductive (cf. Reductive group).
is reductive (cf. Reductive group).
A.L. Onishchik
Comments
References
| [a1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) pp. 283ff |
| [a2] | I. Satake, "Classification theory of semi-simple algebraic groups" , M. Dekker (1971) pp. 32ff |
| [a3] | V.S. Varadarajan, "Lie groups, Lie algebras, and their representations" , Prentice-Hall (1974) |
| [a4] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1 |
Radical of a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Radical_of_a_group&oldid=11973