Quantum Turing machine
2020 Mathematics Subject Classification: Primary: 68Q05 Secondary: 03D10 [MSN][ZBL]
The quantum Turing machine (QTM) is the quantum analogon of a Turing machine (TM). For many aspects, a close analogy to the classical counterpart exists. Though a quantum Turing machine can be defined more or less canonically, several conceptional problems associated with it and concerning the notion of 'quantum computation' exist and are still unsolved. Other properties of the quantum Turing machine like the question, whether universality does hold or not, are unknown as well.
Quantum Aspects of Computation
Church-Turing Thesis
The Church-Turing thesis defines an 'algorithm' as a description of a calculation. But is this the whole story? A calculation is not only a platonic object, usually it is intended to execute the actual calculation in one way or the other. Put in other words, the calculation should be realized physically. Then, the device executing the calculation has to be considered as physical system. A calculation is the execution of a physical experiment, and its result is provided by the observation of the experiment.
Today, many devices executing calculations are known. They are not limited to digital computers. Other types are e.g. analogous computers, soap-bubble based computers, the DNA-computing approach, and the Antikythera mechanism. This leads to the question, whether the restriction to classical models of computation like Turing machines is really adequate.
Church-Turing-Deutsch Thesis
The idea of the Turing machine dates back to the year 1936. At this time, the physical world seemed to be dominated by mechanical forces; correspondingly, the definition of a Turing machine is based on the ideas of classical mechanics. And though the physical realization of a Turing machine, the digital computer, actually uses quantum mechanics, its construction principles aims at the suppression of any effect associated with the quantum world. With ever-tighter package density, however, this is not achievable anymore in a perfect way. The effects of quantum theory may begin to have an influence on the outcome of the calculation.
Considered from another perspective, computations executed by humans are mental processes. In this way, the Church-Turing thesis is also a statement about the human mind. The Platonic world (including computations) is a mental construction. The brain, which is generating the Platonic world, is a physical system in turn; and at the microscopic level, this system has a quantum mechanical nature.
Consequently it seems to be questionable whether the Turing machine provides a 'natural' model of computation. Searching for alternatives and taking the quantum nature of the world into consideration, Feynman has the idea of quantum computation in 1982. As model executing such a quantum computation, he proposes the quantum Turing machine as quantum theoretical analogon to the Turing machine. Similar ideas were developed independently by Yuri Manin in 1980. Accordingly, David Deutsch generalized the Church-Turing thesis to the Church-Turing-Deutsch thesis in 1985, which states that every computation, which can be realized physically, can be executed using a quantum Turing machine.
Quantum Measurements
This section summarizes basic properties of quantum measurements. They are the necessary prerequisite for the discussion of quantum Turing machines. In order to simplify the following considerations, we will make two assumptions.
- The eigenspaces are not degenerated
- The operators associated with measurements have a discrete spectrum
These assumptions help us to concentrate on the foundations instead of technicalities.
Let us now consider a measurement executed by applying an observable $\hat O=|\psi_i \rangle\langle \psi_i |$ having an Eigenvalue $a_i$ with a corresponding Eigenvector $| \psi_i\rangle$. The probability $p$ of measuring the Eigenvalue $a_i$ in a state $| \psi\rangle=\sum_l \alpha_l | \psi_l\rangle \in\mathcal{H}$ is given by $p=|\langle \psi_i |\psi\rangle|^2= |\alpha_i|^2$. When measuring the Eigenvalue $a_i$, the original state $| \psi\rangle$ is changed to the corresponding Eigenvector $| \psi_i\rangle\in\mathcal{H}$ as new quantum state.
Quantum theory would not be probabilistical without measurements. The probabilistic nature could be explained as a result of an interaction between the measurement system and the quantum system, which leads to an entanglement of states. Consequently, the quantum system does not evolve independent from the outside world anymore, its future state is influenced by the measurement system.
Example: Qubits
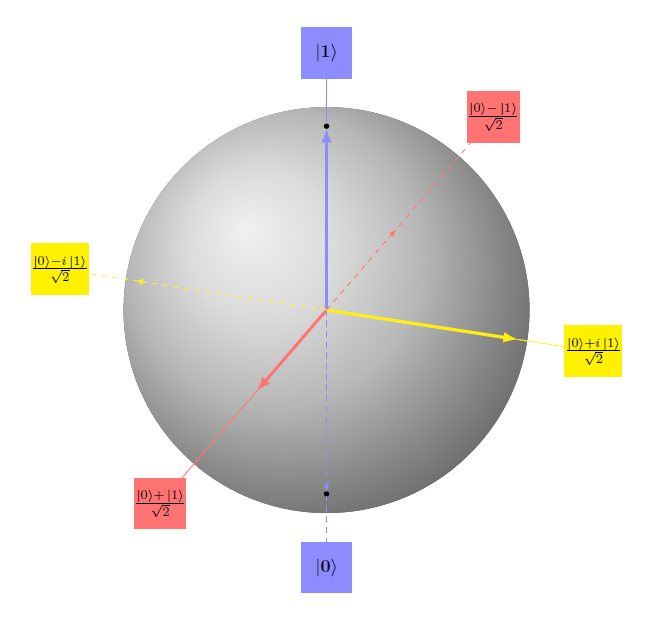
A Qubit represents a quantum state $Q$ having 2 ground states $\{0,1\}$. Accordingly, $Q$ is given by $$ Q= \alpha | 0\rangle + \beta | 1\rangle.$$ This leads to a 2-dimensional Hilbert-space $\mathcal{H}\cong \mathbb{C}^2$. The probabilities of measuring the ground states are equal to $|\alpha|^2$ and $|\beta|^2$. It holds $ |\alpha|^2 + |\beta|^2 = 1 $, i.e. for example $$Q=\frac{1}{\sqrt{2}}| 0\rangle - \frac{1}{\sqrt{2}}| 1\rangle.$$
The situation described here is not identical with a random bit having values $\{0,1\}$ and probabilities $|\alpha|^2 $, $|\beta|^2$. Whereas a total of 4 different transformations can explain all possible transformations of a random bit, a Qubit can be transformed in infinitely many ways. The possible transformations applied on a Qubit can be represented by rotations of a so-called Bloch sphere.
Definition of a Quantum-Turing-Machine
From Classical to Quantum Dynamics
The basic construction of a quantum Turing machine resembles the classical Turing machine. We assume an infinite tape and the existence of a read/write head. With exception of the transition function $\delta$, all other components of the definition can be reformulated canonically.
- $Q=\{q_i\}_i$, finite state set
- $\Sigma=\{\sigma_j\}_j$, finite input alphabet
- $\Gamma=\{\gamma_k\}_k$, finite tape alphabet
- $\sqcup\in \Gamma$, blank symbol with $\sqcup \notin \Sigma$
- $q_0\in Q$, start state
- $F \subseteq Q$, set of end states
Lance Fortnow (2003) has developed a formalism, which unifies the definitions of a classical Turing machine, a nondeterministic Turing machine, a probabilistic Turing machine, and a quantum Turing machine. His formalism addresses the aspects of the dynamics, which can not be canonically translated to the quantum level. The problem is that the transition function $\delta$ of a Turing machine has the form $\delta\colon Q\times\Sigma\to Q\times\Sigma \times \{L,R,N\}$, wherein the expression $\{L,R,N\}$ does not represent a set of states but a set of head actions. As a way-out, Fortnow proposes a representation of $\delta$ as transition matrix in the space $(q,B,i)\in Q\times \Gamma^\ast \times \mathbb{Z}=:C$ of configurations. The actual configuration, which consists of the (local) state of the Turing machine, the content of its tape, and the position of its head on the tape, provides some kind of global state of the Turing machine. Accordingly, the set $C=\{c_i\}_{i\in I}$ of configurations is used for representing the ground states of the physical system. Assuming $c_i=(\ldots,0,1,0,\ldots)^t$, $\delta\colon c_i\mapsto c_j$ becomes a transition function operating on $C$ representable as a matrix $U$: $$U_{ji} := \begin{cases} 1 & \text{$c_i \buildrel \delta\over\longrightarrow c_j$}\\ 0 & \text{otherwise} \end{cases} $$ The permutation property $U \cdot c_i = c_j$ resembles the (classical) Turing machine. If instead of $U_{ij}\in\{0,1\}$ a probability matrix with $U_{ij}\in \mathbb{R}$ is used, the case of a probabilistic Turing machine is resembled. For the case of a quantum Turing machine $M$, a unitary matrix $U$ is chosen with $U_{ij}\in \mathbb{C}$. The matrix $U$ represents an operator $\hat U$ describing the quantum dynamics of $M$. Due to the property of unitarity, the dynamics must be reversible. It determines the 'program' of $M$. A computation step of $M$ has the form $| \psi(n+1)\rangle=\hat U | \psi(n)\rangle= \hat U^{n+1}| \psi(0)\rangle$. According to its construction, $\hat U$ changes the content of the quantum 'tape' only at the position $i$ of the head. Furthermore, $\hat U$ moves the head at most one step to the right or to the left. Due to $U_{ij}\in \mathbb{C}$, interference is possible with amplification and extinction. The notion of superposition becomes relevant, leading to interdependences between states.
David Deutsch (1985) completed the construction of a quantum Turing machine using the results of Lance Fortnow. In the quantum analogon, a configuration $\psi=(q,B,i)\in C$ is interpreted as (ground) state $| \psi\rangle =|q\rangle|B\rangle|i\rangle$. This gives the countable base of the corresponding Hilbert space. For an input $x$, the start configuration $c_{{\mathrm{init}}(x)}$ of the quantum Turing machine is represented by $| \psi(0)\rangle= | q_0\rangle | x\rangle| 1\rangle$ and with exception of $x$, the tape is empty.
Observables of a quantum Turing machine
After the halt of the machine, one has to execute measurements for determining the symbols at the tape positions. For the set $Q=\{q_0, \ldots, q_r\}$ of states and the set $\Gamma=\{\gamma_1,\ldots,\gamma_s\}$ of tape symbols the observables are
- $\hat q =\sum\limits_{l=0}^r l |q_l\rangle\langle q_l|$ for the actual state.
- $\hat B(m) =\sum\limits_{l=0}^s l |\gamma_l\rangle\langle \gamma_l|$ with $m\in\mathbb{Z}$ for the actual tape symbol at the tape position $m$. Since we assume a computation of finite length, we have to measure only the contents of a finite number of $m\in\mathbb{Z}$.
- $\hat \zeta =\sum\limits_{\zeta\in\mathbb{Z}} \zeta |\zeta\rangle\langle \zeta|$ for the actual head position.
The Input of a quantum Turing machine is a classical state and thus reproducable. Furthermore, the dynamics of a QTM is deterministical; thus the computation steps of quantum Turing machines can be reproduced as well. Reading out the result of the computation, which is realized by executing a measurement, is probabilistic in the contrary. Given the input $x$, the probability of reaching a specific accepting configuration $c_{\mathrm{accept}}$ after $n$ computation steps is equal to $| {{\langle {c_{{\mathrm{accept}}}}|}U^n| c_{{\mathrm{init}}(x)}\rangle}|^2$. Despite of randomized measurement results, one can control the correctness of the result in the case of $P$('correct' result) $=1/2+\varepsilon$, $\varepsilon > 0$, due to the determinism of the dynamics. 'Wrong' results can not be excluded, however.
Computability of Coefficients $U_{ij}$
Choosing continuous coefficients $U_{ij}\in\mathbb{C}$ does not destroy the discrete nature of quantum computation according to the argument, that for a finite number of computation steps a finite precision of $U_{ij}$ will suffice. This statement seems to be doubtful, however, if e.g. physical systems showing quantum chaos should be simulated for time intervals of arbitrary length. Such a situation requires the bookkeeping of system parameters with infinite precision. Similarly, simulations associated with the property of universality are conceptually nontrivial as well. Let $M$ be a quantum Turing machine with evolution operator $\hat U$ represented by a natrix $U_{ij}$. The simulation of $M$ by a universal quantum Turing machine $T$ requires the computability of the matrix coefficients $U_{ij}$ due to the following reasons:
- If a coefficient $U_{ij}$ is a noncomputable object, it could be used by $T$ as an oracle. A seemingly universal behavior of $T$ may then not realized by simulation as intended but by encoding the simulation behavior in the coefficients $U_{ij}$.
- Admitting noncomputable $U_{ij}$ would lead to uncountably many quantum Turing machines. This would exclude their representation by a single discrete universal quantum Turing machine.
- Another counting argument is based on the fact that a noncomputable $U_{ij}$ is not finitely describable; it has $\infty$ many digits. Thus, the quantum Turing machine $M$ is not finitely describable either.
The restriction to computable $U_{ij}$ is no significant restriction. Let $\bar{\mathbb{C}}\subseteq \mathbb{C}$ be the subset of (quantum) computable coefficients. This set is closed w.r.t. quantum computation operations. For example, $U_{ij}\in\bar {\mathbb{R}}$ leads immediately to $\sin U_{ij}, \cos U_{ij}\in\bar{\mathbb{R}}$ due to the possible application of rotation matrices. Since all elements of $\mathbb{Q}$ are computable, it holds $\bar{\mathbb{C}}\subseteq^{\text{dense}} \mathbb{C}$. Thus all $U_{ij}\in \mathbb{C}$ are approximable by elements of the set $\bar {\mathbb{C}}$. In principle, it is even possible to use much more restricted number domains for the coefficients $U_{ij}$ without restricting the computable power. Such a limitation of the number domain may lead to an increase of the computational complexity, however.
Properties of a Quantum-Turing-Machine
Quantum Complexity
$\mathrm{BQP}$ designates a complexity class called Bounded-Error Quantum Polynomial Time. $L\in\mathrm{BQP}$ means that it exists a quantum Turing machine with \begin{align*} \forall x\in L\colon & \,\, |{\langle {C_{\mathrm{accept}}}|} U^n| c_{{\mathrm{init}}(x)}\rangle|^2 \ge 2/3\\ \forall x\notin L\colon & \,\, |{\langle {C_{\mathrm{accept}}}|} U^n| c_{{\mathrm{init}}(x)}\rangle|^2 < 1/3 \end{align*} and $n$ is growing polynomial with $|x|$, whereby $C_{\mathrm{accept}}$ designates the set of all accepting configurations.. It holds ${\mathrm{BPP}}\subseteq \mathrm{BQP}$, but the validity of the relation ${\mathrm{BPP}}\subset \mathrm{BQP}$ is unknown.
As a second example of a quantum complexity class, consider ${\mathrm{NQP}}$. A language $L\in{\mathrm{NQP}}$ belongs to this class if it exists a quantum Turing machine $M$ with \begin{align*}\forall x\in L\colon & \,\, \mathrm{Prob}[M(x)\ {\mathrm{accepts}}] > 0\\ \forall x\notin L\colon & \,\, \mathrm{Prob}[M(x)\ {\mathrm{accepts}}] = 0\end{align*} In the general, a quantum state is a superposition of ground states. Specific superpositions can be constructed by probabilistic combinations of unitary operators. The possibility of using superpositions for parallel computations does not necessarily imply the usability of quantum parallelism, however, since it is not possible to measure linear combinations due to missing corresponding observables. If a measurement of a quantum state $| \psi\rangle$ by an operator $\hat O$ gives an eigenvector $| i\rangle\in\mathcal{H}$, another measurement of $\hat O$ gives $| i\rangle\in\mathcal{H}$ again with probability $p= 1$. The measurement influences (destroys) the original quantum state $| \psi\rangle$. As a consequence, a superposition can not be observed.
This means that a potential complexity advantage exist, but may be unusable in practice. In other words, for a language $L\in \mathrm{NX}$ being a member of a nondeterministic complexity class $\mathrm{NX}$, it does not necessarily hold $L\in (B)\mathrm{QX}$ as well. The term $(B)\mathrm{QX}$ designates the (bounded-error) quantum complexity class associated with the nondeterministic complexity class $\mathrm{NX}$. Specifically, it is still unknown whether a quantum Turing machine can solve ${\mathrm{NP}}$-problems in $\mathrm{BQP}$.
On the other hand, it is still unknown whether it does hold ${\mathrm{NP}}={\mathrm{P}}$ or not at the classical level. If yes, ${\mathrm{NP}}$-problems can be solved efficiently without using a quantum Turing machine. Actually, it is still unknown, whether using a QTM instead of a TM accelerates the computation superpolynomially or not. Up to now, only examples of a polynomial acceleration are known (e.g. Grovers Algorithm, Simons Algorithm).
Simulation of Classical Algorithms
For constructing a quantized version of a classical algorithm $A$, one has to take care about the peculiarities of quantum theory. It is essential for a quantum Turing machine to have a reversible transition function. Reversibility can be assured e.g. by preserving the input $x$ $$(x,x){\buildrel\delta\over\longrightarrow} (x,A(x)).$$ On the other hand, a quantum Turing machine can be simulated by a Turing machine as well. This shows that no extended computability exists on the quantum level.
Simulation of Quantum Systems
The simulation of quantum systems may be an important application of quantum computation. This topic is of theoretical interest as well, since the notion of universality relies on the notion of simulability. Let us consider a quantum system with $n$ states and $k$ different values for each state. A simulation at the classical level is necessarily inefficient, because every combination of states has to be considered separately. Thus $k^n$ coefficients $\alpha_i$ have to be stored and processed separately. At the quantum level, however, a simulation may be efficient, since using a superposition all $k^n$ state combinations can be processed simultaneously. Put in another way, using a superposition means a simultaneous processing of an exponential number of states.
Example: Qubits
The state space of a combination of $N$ Qubits has dimension $2^N$. This means that the amount of informations grows exponentially with the number of particles. Let us consider an example: For 2 Qubits the overall quantum state can be represented as $|\psi\rangle = \alpha_0 |00\rangle + \alpha_1 |01\rangle + \alpha_2 |10\rangle + \alpha_3 |11\rangle$. The system is composed of 2 quantum objects designated as $| \psi_1\rangle,| \psi_2\rangle$. Due to interactions in the past, $| \psi_1\rangle,| \psi_2\rangle$ may be eventually not independent from each other. They may have common informations, which are locally not accessible, e.g. $$| \psi\rangle=\frac{1}{\sqrt{2}}| 00\rangle + \frac{1}{\sqrt{2}}| 11\rangle.$$ If the measurement of $| \psi\rangle$ gives 1, then $| \psi' \rangle$ gives 1 as well. This is an example of entanglement: The measurement of $| \psi' \rangle$ determines $| \psi\rangle$ as well. If it holds $| \psi\rangle= c_2\cdot | 01\rangle+c_4\cdot | 11\rangle$, no entanglement exists in QuBit II in the contrary.
Comparision of Turing machines
'Classical' Turing machines
Here, we consider both deterministic and nondeterministic Turing machines. For a deterministic Turing machine, a superposition of states is not allowed. At each time, only a single state is active. A nondeterministic Turing machine, in the contrary, allows some kind of state superposition. The resulting capability of processing different branches of the computation simultaneously may give the nondeterministic Turing machine a complexity advantage. Both types of Turing machines provide a single specific value as result after a certain number of computation steps. The simulation property (e.g. for checking universality) is formulated as an equality based on a value to value correspondence.
Probabilistic Turing machines
Probabilistic Turing machines are using random combinations of states. Accordingly, the machine gives a probability distribution of possible outcomes as result, though the computation, which will lead to this result, consists of a concrete number of steps. For a probabilistic Turing machine, the simulation property (e.g. for checking universality) is based on an equality between probability distributions.
Quantum Turing machines
Different from other kind of Turing machimes, a quantum Turing machine may perform a varying number of computation steps for a specific input because of the necessary measurement of the validity of a halting condition. Despite of the random nature of the measurement of the computation result, the calculated output consists of a single concrete value. The result of the calclulation has to be defined based on statistical sampling. Though this will be an unpleasant complication in most cases, it offers also an option for a direct realization of probabilistic algorithms. Especially, the creation of true random numbers become possible in the context of quantum Turing machines.
A quantum Turing machine is acting on states $\psi$, not on probabilities $|\psi|^2$ like probabilistical Turing machines. This is of great importance, because states are carrying more informations than probabilities. Whereas classical probability is measured using the $L_1$-Norm, quantum probability is measured using the $L_2$-Norm according to $p=|\psi|^2$.
Conceptual Problems of quantum Turing machines
Universality of quantum Turing machines
According to the Church-Turing-Deutsch thesis, computations are not (only) theoretic constructs but should be actually executable. This does affect the notion of 'universality'. How we can simulate another quantum Turing machine after finishing the simulation of the first one? Especially, how a new input is given to a quantum Turing machine supposed to be universal? One of the problems to be solved in this respect is how an empty tape can be assured. Remember, that the machine continues to process during the 'deletion' operation. A possible solution is to make use of reversibility. But when to stop rollback?
Another problem is the probabilistic nature of the results of a quantum Turing machine. According to its definition, it can be checked only approximately (using statistical sampling) whether two machines have the same behavior. This is a problem, when the validity of an infinite number of behavior coincidences must be verified. Let $n_x$ be the number of computation steps necessary for reaching an approximation error $< \varepsilon$ for the input $x$. The number $n_x$ will of course be different for different $x$. Assuming $n_x\rightarrow \infty$ for $|x| \rightarrow \infty$, is the check of behavior coincidence still computable? Due to such problems, the existence of a universal quantum Turing machine has still to be confirmed.
Parallelism in a quantum Turing machine
A quantum Turing machine is rather unique concerning the necessity of measurements. This may require additional constraints for the quantum evolution of such a machine when well-definedness should be assured in the presence of superpositions and quantum parallelism.
- Requirement I
- The head of the quantum Turing machine should have the same position for each computation step and for all branches of a compiutation. Otherwise the principle of locality could be violated.
- Requirement II
- The predicate $q\in F$ of the actual state $q\in Q$ of the quantum Turing machine should have the same value for all branches of an eventual quantum parallelism for each computation step. Otherwise, the halt of the quantum Turing machine would not be well-defined.
These requirements for the operation of a quantum Turing machine will lead immediatly to corresponding requirements for quantum algorithms as well. It is unknown up to now, which consequences these requirements will have in turn on the complexity of quantum algorithms. Furthermore, according to a theorem proven by Miyadera & Ohya it is undecidable whether a quantum Turing machine $M$ fulfills requirement II or not.
Halting of a quantum Turing machine
The 'halt' of a quantum Turing machine is very different from the halt of a classical Turing machine. Quantum dynamics can never 'stop'. Thus formulating a suitable definition of halting is a challenging task, which is not yet satisfactory solved.
One option is to understand a 'halt' as a situation in which the actual configuration remains unchanged. This would be a contradiction to the fundamental property of reversibility, however. An alternative is to check whether the quantum Turing machine has reached a final state $q_f \in F$ by measuring the observable $|q_f\rangle\langle q_f|$. Unfortunately, the actual state $q(t)\in Q$ of the machine can be influenced by measurements. The determinism of quantum dynamics is given up when the computation process is intertwined with sporadic measurements.
References
| [A2005] | Scott Aaronson, "Quantum computing, postselection, and probabilistic polynomial-time", Proceedings of the Royal Society A461(2005)3473-3482 |
| [A2013] | Scott Aaronson, "The Ghost in the Quantum Turing Machine", arXiv:1306.0159v2 [quant-ph] |
| [BC2006] | D.P. Bovet, P. Crescenzi, "Introduction to the theory of complexity", Lecture Notes, unpublished 2006 |
| [CC2010] | Goong Chen, David A. Church, Berthold-Georg Englert, Carsten Henkel, Bernd Rohwedder, Marlan O. Scully, M. Suhail Zubairy, "Quantum Computing Devices: Principles, Designs, and Analysis", CRC Press 2010 |
| [D1985] | David Deutsch, "Quantum theory, the Church-Turing principle and the universal quantum computer", Proceedings of the Royal Society of London A400(1985)97-117 |
| [F2003] | Lance Fortnow, "One Complexity Theorist's View of Quantum Computing", Theoretical Computer Science 292(3)(2003)597-610 |
| [F2007] | Willem Fouché, Johannes Heidema, Glyn Jones, Petrus H. Potgieter, "Deutsch's Universal Quantum Turing Machine (Revisited)", arXiv:0701108v1 [quant-ph] |
| [H1997] | Mika Hirvensalo, "On Quantum Computation", Licentiate's thesis, University of Turku 1997 |
| [M1980] | Yuri Manin, "Vychislimoe i nevychislimoe", Sov.Radio. 1980 |
| [MN1994] | Takashi Mihara, Tetsuro Nishino, "On a Method of Solving NP-Complete Problems in Polynomial Time Using the Quantum Turing Machine", in Maruoka, Akira (editor), "Computational complexity theory", Proceedings of a symposium held at Kyoto 1994, in RIMS Kokyuroku 871(1994)30-36 |
| [M2012] | Jaroslaw Miszczak, "High-Level Structures for Quantum Computing", Morgan & Claypool Publishers 2012 |
| [MO2002] | Takayuki Miyadera, Masanori Ohya, "Designing Quantum Turing Machine is uncomputable", in Proceeedings of the Erato Workshop on Quantum Information Science 2002 |
| [MO2005] | Takayuki Miyadera, Masanori Ohya, "On Halting Process of Quantum Turing Machine", Open Systems and Information Dynamics, 12(3)(2005)261-265 |
| [M2007] | Markus Müller, "Quantum Kolmogorov Complexity and the Quantum Turing Machine", PhD Thesis, Technischen Universität Berlin 2007 |
| [ON2000] | Masanao Ozawa, Harumichi Nishimura, "Local Transition Functions of Quantum Turing Machines", Theoret. Informatics and Appl. 34(2000)379-402 |
| [P2011] | Simon Perdrix, "Partial Observation of Quantum Turing Machine and Weaker Well-Formedness Condition", Electronic Notes in Theoretical Computer Science 270, Issue 1, (2011) pp. 99-111, also in B. Coecke, I. Mackie, P. Panangaden, P. Selinger (editors), Proceedings of the Joint 5th International Workshop on Quantum Physics and Logic and 4th Workshop on Developments in Computational Models QPL/DCM 2008 |
| [P2006] | P. Prashant, "The Church-Turing-Deutsch Principle in Quantum Computation", in Hamid R. Arabnia, Mark Murgin (Eds.), Proceedings of the 2006 International Conference on Foundations of Computer Science, Las Vegas 2006, CSREA Press 2006, pp. 141-148 |
| [S2000] | A. Stern, "Quantum Theoretic Machines: What is thought from the point of view of Physics?", Elsevier 2000 |
| [Y1993] | Andrew Yao, "Quantum circuit complexity", Proceedings of the 34th Annual Symposium on Foundations of Computer Science, 1993, pp. 352-361 |
Quantum Turing machine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_Turing_machine&oldid=31935