Pseudo-metric
on a set 
A non-negative real-valued function 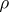 defined on the set of all pairs of elements of
defined on the set of all pairs of elements of 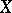 (that is, on
(that is, on 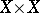 ) and subordinate to the following three restrictions, called the axioms for a pseudo-metric:
) and subordinate to the following three restrictions, called the axioms for a pseudo-metric:
a) if 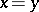 , then
, then 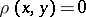 ;
;
b) 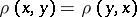 ;
;
c)  , where
, where  ,
, 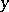 and
and  are arbitrary elements of
are arbitrary elements of 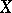 .
.
It is not required that 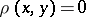 implies
implies  . A topology on
. A topology on 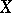 is determined as follows by a pseudo-metric
is determined as follows by a pseudo-metric 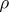 on
on 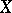 : A point
: A point  belongs to the closure of a set
belongs to the closure of a set 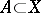 if
if 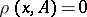 , where
, where
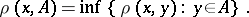 |
This topology is completely regular but is not necessarily Hausdorff: singleton sets can be non-closed. Every completely-regular topology can be given by a collection of pseudo-metrics as the lattice union of the corresponding pseudo-metric topologies. Analogously, families of pseudo-metrics can be used in defining, describing and investigating uniform structures.
References
| [1] | J.L. Kelley, "General topology" , Springer (1975) |
Comments
See also Metric and Quasi-metric.
References
| [a1] | E. Čech, "Topological spaces" , Interscience (1966) pp. 532 |
Pseudo-metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-metric&oldid=29453