Pseudo-Riemannian space
A space with an affine connection (without torsion), at each point of which the tangent space is a pseudo-Euclidean space.
Let  be an
be an  -space with an affine connection (without torsion) and let
-space with an affine connection (without torsion) and let  be the tangent pseudo-Euclidean space at every point of
be the tangent pseudo-Euclidean space at every point of  ; in this case the pseudo-Riemannian space is denoted by
; in this case the pseudo-Riemannian space is denoted by  . As in a proper Riemannian space the metric tensor of
. As in a proper Riemannian space the metric tensor of  is non-degenerate, has vanishing covariant derivative, but the metric form of
is non-degenerate, has vanishing covariant derivative, but the metric form of  is a quadratic form of index
is a quadratic form of index  :
:
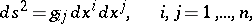 |
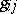 is the metric tensor of
is the metric tensor of 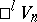 ,
, 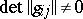 . The space
. The space 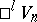 can be defined as an
can be defined as an  -dimensional manifold on which an invariant quadratic differential form of index
-dimensional manifold on which an invariant quadratic differential form of index 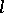 is given.
is given.
The simplest example of a pseudo-Riemannian space is the space 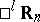 .
.
The pseudo-Riemannian space 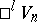 is said to be reducible if in a neighbourhood of each point there is a system of coordinates
is said to be reducible if in a neighbourhood of each point there is a system of coordinates 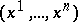 such that the coordinates
such that the coordinates 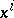 can all be separated into groups
can all be separated into groups 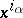 such that
such that  only for those indices
only for those indices 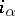 and
and 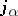 which belong to a single group and the
which belong to a single group and the 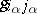 are functions only of the coordinates of this group.
are functions only of the coordinates of this group.
In a pseudo-Riemannian space the sectional curvature is defined for every non-degenerate two-dimensional direction. It can be interpreted as the curvature of the geodesic (non-isotropic)  -surface drawn through the given point in the given two-dimensional direction. If the value of the curvature at each point is the same for all two-dimensional directions, then it is constant at all points (Schur's theorem), and in this case the space is said to be a pseudo-Riemannian space of constant curvature
-surface drawn through the given point in the given two-dimensional direction. If the value of the curvature at each point is the same for all two-dimensional directions, then it is constant at all points (Schur's theorem), and in this case the space is said to be a pseudo-Riemannian space of constant curvature 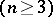 . An example of a pseudo-Riemannian space of constant negative curvature is the hyperbolic space
. An example of a pseudo-Riemannian space of constant negative curvature is the hyperbolic space 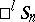 of negative curvature — it is a pseudo-Riemannian space
of negative curvature — it is a pseudo-Riemannian space 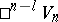 ; the space
; the space 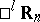 is a pseudo-Riemannian space of vanishing curvature.
is a pseudo-Riemannian space of vanishing curvature.
References
| [1] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [2] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
| [3] | A. Einstein, "Collected scientific works" , 1 , Moscow (1965) (In Russian; translated from English) |
Comments
Important for applications in physics is the case of index 1. For any  ,
, 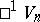 is called a Lorentzian manifold. Here the tangent vectors having purely imaginary, vanishing or non-vanishing real length are called time-like, light-like or space-like, respectively. If
is called a Lorentzian manifold. Here the tangent vectors having purely imaginary, vanishing or non-vanishing real length are called time-like, light-like or space-like, respectively. If 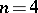 and
and 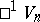 possesses a global time-like vector field, then
possesses a global time-like vector field, then 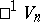 is called a space-time and admits a distinction between future and past. Such a space-time is the general geometric model in which the phenomena of the theory of general relativity are described. For example, the history of a material or light-like particle is described by a world-line having non-space-like tangents only. The coupling between the geometric model and the physical data is given by Einstein's field equations (cf. Einstein equations).
is called a space-time and admits a distinction between future and past. Such a space-time is the general geometric model in which the phenomena of the theory of general relativity are described. For example, the history of a material or light-like particle is described by a world-line having non-space-like tangents only. The coupling between the geometric model and the physical data is given by Einstein's field equations (cf. Einstein equations).
During the last decades much progress has been made concerning global Lorentzian geometry. This was initiated by R. Penrose and pursued by S.W. Hawking in particular (see [a2]). The main highlights in this development are the Hawking–Penrose singularity theorems, showing that under special geometric conditions (e.g. non-negative Ricci curvature in time-like directions and the existence of a compact space-like hypersurface with positive mean curvature, or non-negative Ricci curvature in light-like directions and the existence of a non-compact Cauchy hypersurface and a trapped surface) the space-time has a future singularity, i.e. there exists a future-incomplete, causal geodesic. Up to time orientation the standard models for these singularities are the Schwarzschild model (black hole) and the Robertson–Walker–Friedman model (big-bang). See also Cosmological models. The corresponding theory can be found in [a1]–[a4].
References
| [a1] | J.K. Beem, P.E. Ehrlich, "Global Lorentzian geometry" , M. Dekker (1981) |
| [a2] | S.W. Hawking, G.F.R. Ellis, "The large scale structure of space-time" , Cambridge Univ. Press (1973) |
| [a3] | B. O'Neill, "Semi-Riemannian geometry (with applications to relativity)" , Acad. Press (1983) |
| [a4] | R.K. Sachs, H. Wu, "General relativity for mathematicians" , Springer (1977) |
| [a5] | C.W. Misner, K.S. Thorne, J.A. Wheeler, "Gravitation" , Freeman (1973) |
Pseudo-Riemannian space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-Riemannian_space&oldid=13115