Projector
projection operator
A linear operator 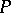 on a vector space
on a vector space  such that
such that 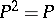 .
.
Comments
In the Western literature often the term projection is used instead of projector. See also Projection.
If 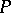 is a projection, so is
is a projection, so is 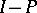 , and together they define a direct sum decomposition
, and together they define a direct sum decomposition 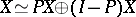 . Conversely, a direct sum decomposition defines a projection. In Banach space theory a projection is usually also required to be bounded. Given a set
. Conversely, a direct sum decomposition defines a projection. In Banach space theory a projection is usually also required to be bounded. Given a set 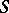 of commuting projections, there is a partial order on
of commuting projections, there is a partial order on 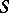 , defined by
, defined by  if and only if
if and only if 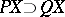 . The intersection and union of two commuting projections
. The intersection and union of two commuting projections 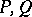 are, respectively, the projections
are, respectively, the projections 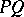 and
and 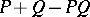 . A Boolean algebra of projections is a set of commuting projections containing the zero and identity operations and which is closed under intersection of projections (i.e., taking the greatest lower bound) and union of projections (i.e., taking the least upper bound). Such Boolean algebras of projections play an important role in (self-adjoint and spectral) operator theory, cf. Spectral measure and [a1].
. A Boolean algebra of projections is a set of commuting projections containing the zero and identity operations and which is closed under intersection of projections (i.e., taking the greatest lower bound) and union of projections (i.e., taking the least upper bound). Such Boolean algebras of projections play an important role in (self-adjoint and spectral) operator theory, cf. Spectral measure and [a1].
References
| [a1] | N. Dunford, J.T. Schwartz, "Linear operators" , Wiley (Interscience) (1988) pp. Chapts. X; XV |
Projector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projector&oldid=18674