Projective limit
inverse limit
A construction that arose originally in set theory and topology, and then found numerous applications in many areas of mathematics. A common example of a projective limit is that of a family of mathematical structures of the same type indexed by the elements of a pre-ordered set. Let 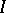 be a set endowed with a pre-order relation
be a set endowed with a pre-order relation 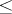 , and suppose that with each element
, and suppose that with each element 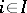 a set
a set 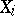 is associated and with each pair
is associated and with each pair  ,
, 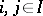 , in which
, in which 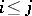 , a mapping
, a mapping 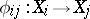 is associated, where the
is associated, where the 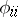 ,
,  , are identity mappings and
, are identity mappings and 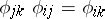 for
for 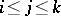 . A set
. A set 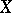 is called a projective limit of the family of sets
is called a projective limit of the family of sets  and mappings
and mappings 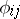 if the following conditions are satisfied: a) there exists a family of mappings
if the following conditions are satisfied: a) there exists a family of mappings 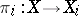 such that
such that 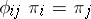 for any pair
for any pair 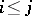 ; b) for any family of mappings
; b) for any family of mappings  ,
, 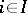 , from an arbitrary set
, from an arbitrary set 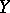 , for which the equalities
, for which the equalities 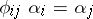 hold for
hold for 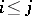 , there exists a unique mapping
, there exists a unique mapping 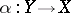 such that
such that 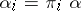 for every
for every 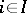 . The projective limit can be described explicitly as follows. One considers the direct product
. The projective limit can be described explicitly as follows. One considers the direct product 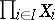 and selects in it the set of all functions
and selects in it the set of all functions 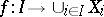 for which the equalities
for which the equalities 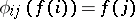 hold for
hold for 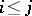 . This subset is the projective limit of the family
. This subset is the projective limit of the family 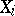 . If all the
. If all the 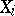 are equipped with an additional structure of the same type and the
are equipped with an additional structure of the same type and the 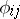 preserve it, then the same structure is induced in the projective limit. Therefore it is possible to speak of projective limits of groups, modules, topological spaces, etc.
preserve it, then the same structure is induced in the projective limit. Therefore it is possible to speak of projective limits of groups, modules, topological spaces, etc.
A natural generalization of this concept of projective limit is that of the projective limit of a functor. Let 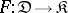 be a functor from a small category
be a functor from a small category 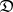 to an arbitrary category
to an arbitrary category 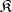 . An object
. An object 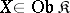 together with morphisms
together with morphisms 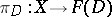 ,
, 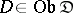 , is called a projective limit (inverse limit, or simply limit) of the functor
, is called a projective limit (inverse limit, or simply limit) of the functor 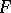 if the following conditions are satisfied:
if the following conditions are satisfied: 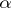 )
) 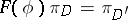 for any morphism
for any morphism 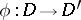 ; and
; and 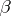 ) for any family of morphisms
) for any family of morphisms 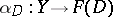 satisfying
satisfying 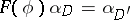 for all
for all 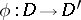 there exists a unique morphism
there exists a unique morphism 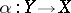 such that
such that 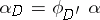 for all
for all 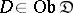 . Notation:
. Notation: 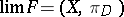 .
.
Examples of projective limits.
1) Let 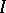 be a discrete category. Then for an arbitrary functor
be a discrete category. Then for an arbitrary functor 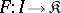 the projective limit of the functor
the projective limit of the functor 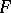 coincides with the product of the family of objects
coincides with the product of the family of objects 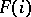 ,
, 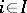 (cf. Product of a family of objects in a category).
(cf. Product of a family of objects in a category).
2) Let 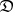 be a category with two objects
be a category with two objects 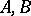 and two non-identity morphisms
and two non-identity morphisms 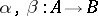 . Then the limit of a functor
. Then the limit of a functor 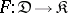 is the equalizer of the pair of morphisms
is the equalizer of the pair of morphisms 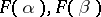 (cf. Kernel of a morphism in a category).
(cf. Kernel of a morphism in a category).
If a category has products of arbitrary small families of objects and equalizers of pairs of morphisms, then it has limits for all functors defined on small categories.
Comments
In most modern work in category theory, the unadorned name "limit" is used for this concept (and the dual concept is called a colimit). The terms "inverse limit" and its dual, direct limit (or inductive limit), are generally restricted to diagrams over directed pre-ordered sets (see Directed order); "projective limit" is best avoided, because of the danger of confusion with the notion of projective object of a category. Inverse and direct limits were first studied as such in the 1930's, in connection with topological concepts such as Čech cohomology; the general concept of limit was introduced in 1958 by D.M. Kan [a1].
References
| [a1] | D.M. Kan, "Adjoint functors" Trans. Amer. Math. Soc. , 87 (1958) pp. 294–329 |
| [a2] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7 |
Projective limit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_limit&oldid=15572