Projective covering
of a module
This is the dual notion of that of an injective envelope or injective hull (cf. Injective module). Let  be an associative ring with unit element,
be an associative ring with unit element,  a left module over
a left module over  . From now on, all modules and morphisms are left modules and morphisms of left modules. An epimorphism
. From now on, all modules and morphisms are left modules and morphisms of left modules. An epimorphism  is an essential epimorphism if the following holds:
is an essential epimorphism if the following holds:  is an epimorphism if and only if
is an epimorphism if and only if  is an epimorphism. This is equivalent to saying that
is an epimorphism. This is equivalent to saying that  is a superfluous submodule, where
is a superfluous submodule, where  is superfluous if for all submodules
is superfluous if for all submodules  one has:
one has: 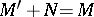 implies
implies  . The notion of an essential epimorphism is dual to that of an essential monomorphism (or essential extension), which is a monomorphism
. The notion of an essential epimorphism is dual to that of an essential monomorphism (or essential extension), which is a monomorphism 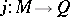 such that
such that  is monomorphic if and only if
is monomorphic if and only if  is monomorphic. A projective covering of
is monomorphic. A projective covering of 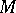 is a projective module
is a projective module  together with an essential epimorphism
together with an essential epimorphism 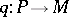 . In contrast to the dual notion of an injective envelope (an injective module
. In contrast to the dual notion of an injective envelope (an injective module 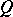 together with an essential monomorphism
together with an essential monomorphism 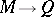 ) projective coverings do not always exist. For instance, indeed especially, projective coverings of Abelian groups (
) projective coverings do not always exist. For instance, indeed especially, projective coverings of Abelian groups (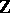 -modules) do not exist. The rings for which projective coverings of modules do exist have been characterized [a1] (cf. also Perfect ring).
-modules) do not exist. The rings for which projective coverings of modules do exist have been characterized [a1] (cf. also Perfect ring).
These notions are completely categorical. A so-called 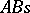 category with generators (also called a Grothendieck category) is such that injective envelopes always exist.
category with generators (also called a Grothendieck category) is such that injective envelopes always exist.
References
| [a1] | H. Bass, "Finitistic homological dimension and a homological generalization of semi-primary rings" Trans. Amer. Math. Soc. , 95 (1960) pp. 466–488 |
| [a2] | N. Popescu, "Abelian categories with applications to rings and modules" , Acad. Press (1973) pp. Sect. 3.10 |
Projective covering. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_covering&oldid=16493