Product of a family of objects in a category

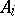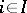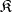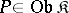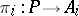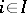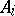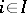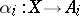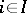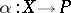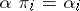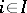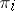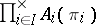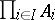A concept characterizing the notion of a Cartesian product in the language of morphisms. Let , , be an indexed family of objects in the category . An object (together with morphisms , ) is called a product of the family of objects , , if for every family of morphisms , , there is a unique morphism such that , . The morphisms are called product projections; the product is denoted by or , or 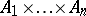in the case 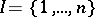. The morphism 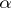that occurs in the definition of the product is sometimes denoted by 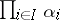or 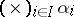. The product of a family 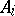, , 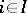is determined uniquely up to isomorphism; it is associative and commutative. The concept of the product of a family of objects is dual to that of a coproduct of a family of objects.

A product of the empty family of objects is a right zero (a terminal object) of the category. In most categories of structured sets (categories of sets, groups, topological spaces, etc.) the concept of the product of a family of objects coincides with the concept of the Cartesian (direct) product of these objects. Nevertheless, this coincidence is not necessary: In the category of torsion Abelian groups the product of a family of groups 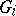, , 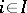is the torsion part of their Cartesian product, which in general is different from the Cartesian product itself.

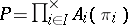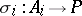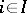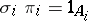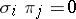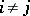In categories with zero morphisms, for any product there exist uniquely defined morphisms , , such that , for . If 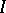is finite and the category is additive, then 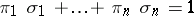and the product of the family of objects 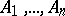is also their coproduct.

References

[1]	M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian)

Comments

S. MacLane [a1] is generally credited with being the first to observe that Cartesian products could be described in purely categorical terms, as above.

References

[a1]	S. MacLane, "Duality for groups" Bull. Amer. Math. Soc. , 56 (1950) pp. 485–516
[a2]	S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7