Principal curvature
The normal curvature of a surface in a principal direction, i.e. in a direction in which it assumes an extremal value. The principal curvatures 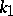 and
and 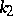 are the roots of the quadratic equation
are the roots of the quadratic equation
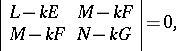 | (*) |
where 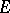 ,
, 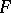 and
and  are the coefficients of the first fundamental form, while
are the coefficients of the first fundamental form, while 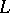 ,
, 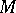 and
and 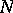 are the coefficients of the second fundamental form of the surface, computed at the given point.
are the coefficients of the second fundamental form of the surface, computed at the given point.
The half-sum of the principal curvatures 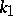 and
and 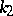 of the surface gives the mean curvature, while their product is equal to the Gaussian curvature of the surface. Equation (*) may be written as
of the surface gives the mean curvature, while their product is equal to the Gaussian curvature of the surface. Equation (*) may be written as
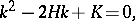 |
where 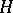 is the mean, and
is the mean, and 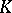 is the Gaussian curvature of the surface at the given point.
is the Gaussian curvature of the surface at the given point.
The principal curvatures 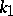 and
and 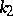 are connected with the normal curvature
are connected with the normal curvature 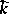 , taken in an arbitrary direction, by means of Euler's formula:
, taken in an arbitrary direction, by means of Euler's formula:
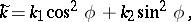 |
where 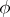 is the angle formed by the selected direction with the principal direction for
is the angle formed by the selected direction with the principal direction for 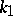 .
.
Comments
In the case of an 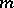 -dimensional submanifold
-dimensional submanifold 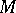 of Euclidean
of Euclidean  -space
-space  principal curvatures and principal directions are defined as follows.
principal curvatures and principal directions are defined as follows.
Let 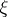 be a unit normal to
be a unit normal to 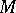 at
at  . The Weingarten mapping (shape operator)
. The Weingarten mapping (shape operator) 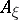 of
of 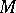 at
at 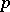 in direction
in direction 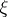 is given by the tangential part of
is given by the tangential part of  , where
, where  is the covariant differential in
is the covariant differential in  and
and 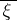 is a local extension of
is a local extension of 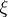 to a unit normal vector field.
to a unit normal vector field. 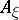 does not depend on the chosen extension of
does not depend on the chosen extension of 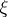 . The principal curvatures of
. The principal curvatures of 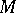 at
at 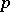 in direction
in direction 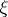 are given by the eigen values of
are given by the eigen values of 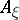 , the principal directions by its eigen directions. The (normalized) elementary symmetric functions of the eigen values of
, the principal directions by its eigen directions. The (normalized) elementary symmetric functions of the eigen values of  define the higher mean curvatures of
define the higher mean curvatures of 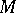 , which include as extremal cases the mean curvature as the trace of
, which include as extremal cases the mean curvature as the trace of 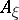 and the Lipschitz–Killing curvature as its determinant.
and the Lipschitz–Killing curvature as its determinant.
References
| [a1] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) |
| [a2] | B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973) |
| [a3] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a4] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a5] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145 |
| [a6] | H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60 |
| [a7] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
| [a8] | B. O'Neill, "Elementary differential geometry" , Acad. Press (1966) |
| [a9] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5 |
Principal curvature. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_curvature&oldid=12102