Primitive root
A primitive root of unity of order 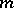 in a field
in a field 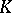 is an element
is an element 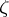 of
of 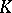 such that
such that 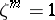 and
and 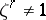 for any positive integer
for any positive integer 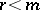 . The element
. The element 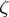 generates the cyclic group
generates the cyclic group 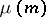 of roots of unity of order
of roots of unity of order 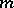 .
.
If in 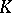 there exists a primitive root of unity of order
there exists a primitive root of unity of order 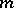 , then
, then 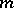 is relatively prime to the characteristic of
is relatively prime to the characteristic of 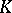 . An algebraically closed field contains a primitive root of any order that is relatively prime with its characteristic. If
. An algebraically closed field contains a primitive root of any order that is relatively prime with its characteristic. If 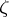 is a primitive root of order
is a primitive root of order  , then for any
, then for any 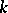 that is relatively prime to
that is relatively prime to  , the element
, the element 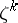 is also a primitive root. The number of all primitive roots of order
is also a primitive root. The number of all primitive roots of order 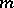 is equal to the value of the Euler function
is equal to the value of the Euler function 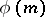 if
if 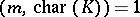 .
.
In the field of complex numbers, the primitive roots of order 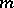 take the form
take the form
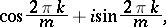 |
where 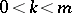 and
and 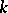 is relatively prime to
is relatively prime to 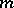 .
.
A primitive root modulo 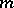 is an integer
is an integer 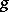 such that
such that
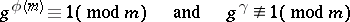 |
for 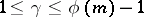 , where
, where 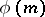 is the Euler function. For a primitive root
is the Euler function. For a primitive root 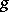 , its powers
, its powers 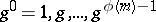 are incongruent modulo
are incongruent modulo 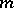 and form a reduced residue system modulo
and form a reduced residue system modulo 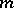 (cf. Reduced system of residues). Therefore, for each number
(cf. Reduced system of residues). Therefore, for each number  that is relatively prime to
that is relatively prime to 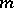 one can find an exponent
one can find an exponent 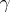
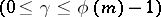 for which
for which 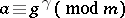 .
.
Primitive roots do not exist for all moduli, but only for moduli 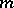 of the form
of the form 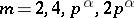 , where
, where 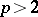 is a prime number. In these cases, the multiplicative groups (cf. Multiplicative group) of reduced residue classes modulo
is a prime number. In these cases, the multiplicative groups (cf. Multiplicative group) of reduced residue classes modulo 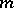 have the simplest possible structure: they are cyclic groups of order
have the simplest possible structure: they are cyclic groups of order 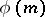 . The concept of a primitive root modulo
. The concept of a primitive root modulo 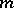 is closely related to the concept of the index of a number modulo
is closely related to the concept of the index of a number modulo 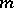 .
.
Primitive roots modulo a prime number were introduced by L. Euler, but the existence of primitive roots modulo an arbitrary prime number was demonstrated by C.F. Gauss (1801).
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1984) |
| [2] | C.F. Gauss, "Disquisitiones Arithmeticae" , Yale Univ. Press (1966) (Translated from Latin) |
| [3] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) |
Primitive root. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primitive_root&oldid=18612