Primary decomposition
A representation of an ideal 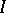 of a ring
of a ring 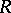 (or of a submodule
(or of a submodule 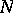 of a module
of a module 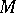 ) as an intersection of primary ideals (primary submodules, cf. Primary ideal). The primary decomposition generalizes the factorization of an integer into a product of powers of distinct prime numbers. The existence of primary decompositions in a polynomial ring was proved by E. Lasker [1], and in an arbitrary commutative Noetherian ring by E. Noether [2]. Let
) as an intersection of primary ideals (primary submodules, cf. Primary ideal). The primary decomposition generalizes the factorization of an integer into a product of powers of distinct prime numbers. The existence of primary decompositions in a polynomial ring was proved by E. Lasker [1], and in an arbitrary commutative Noetherian ring by E. Noether [2]. Let 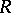 be a commutative Noetherian ring. A primary decomposition
be a commutative Noetherian ring. A primary decomposition 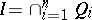 is called irreducible if
is called irreducible if 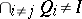 for any
for any 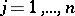 and if the radicals
and if the radicals 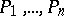 of the ideals
of the ideals 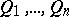 are pairwise distinct (the radical of a primary ideal
are pairwise distinct (the radical of a primary ideal 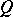 is the unique prime ideal
is the unique prime ideal 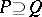 such that
such that 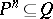 for some natural number
for some natural number  ). The set of prime ideals
). The set of prime ideals 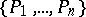 is uniquely determined by the ideal
is uniquely determined by the ideal 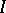 (the first uniqueness theorem for primary decompositions). The minimal elements (with respect to inclusion) of this set are called the isolated prime ideals of
(the first uniqueness theorem for primary decompositions). The minimal elements (with respect to inclusion) of this set are called the isolated prime ideals of 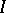 , the other elements are called the imbedded prime ideals. The primary ideals corresponding to isolated prime ideals are also uniquely determined by
, the other elements are called the imbedded prime ideals. The primary ideals corresponding to isolated prime ideals are also uniquely determined by 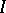 (the second uniqueness theorem for primary decompositions, cf. [3]). The isolated prime ideals of an ideal
(the second uniqueness theorem for primary decompositions, cf. [3]). The isolated prime ideals of an ideal 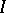 of a polynomial ring over a field correspond to the irreducible components of the affine variety of roots of
of a polynomial ring over a field correspond to the irreducible components of the affine variety of roots of 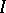 . There are various generalizations of the notion of primary decomposition. The axiomatization of primary decompositions led to the development of the additive theory of ideals.
. There are various generalizations of the notion of primary decomposition. The axiomatization of primary decompositions led to the development of the additive theory of ideals.
References
| [1] | E. Lasker, "Zur Theorie der Moduln und Ideale" Math. Ann. , 60 (1905) pp. 20–116 |
| [2] | E. Noether, "Idealtheorie in Ringbereichen" Math. Ann. , 83 (1921) pp. 24–66 |
| [3] | M.F. Atiyah, I.G. Macdonald, "Introduction to commutative algebra" , Addison-Wesley (1969) |
| [4] | O. Zariski, P. Samuel, "Commutative algebra" , 1–2 , Springer (1975) |
| [5] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Primary decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primary_decomposition&oldid=14571