Pre-orderable group
A group for which any partial order on it may be extended to a total order (cf. Orderable group). A pre-orderable group is also called an  -group. A group is or is not a pre-orderable group in accordance with the following criterion. Let
-group. A group is or is not a pre-orderable group in accordance with the following criterion. Let  be the minimal invariant sub-semi-group of a group
be the minimal invariant sub-semi-group of a group 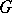 containing an element
containing an element  .
.  will then be pre-orderable if and only if, for any
will then be pre-orderable if and only if, for any  ,
,  does not contain the unit of
does not contain the unit of  and if for any
and if for any  the intersection
the intersection 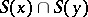 is non-empty.
is non-empty.
All torsion-free nilpotent groups, as well as all orderable two-step solvable groups, are pre-orderable. Free groups of rank higher than 2 and free solvable groups of a solvability class higher than 2 are examples of orderable groups which are not pre-orderable. The local theorem (cf. Mal'tsev local theorems) applies to pre-orderable groups, i.e. if all finitely-generated subgroups of a group 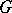 are pre-orderable,
are pre-orderable, 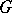 will be pre-orderable as well. However, a subgroup of a pre-orderable group need not be pre-orderable. If a quotient group of a pre-orderable group is orderable, it is pre-orderable. There exist orderable groups which are not pre-orderable, but whose quotient groups by their centres are pre-orderable. The class of pre-orderable groups is closed with respect to direct products but not with respect to complete direct products, and is consequently non-axiomatizable (cf. Axiomatized class). A wreath product of pre-orderable groups is not always pre-orderable. A subgroup
will be pre-orderable as well. However, a subgroup of a pre-orderable group need not be pre-orderable. If a quotient group of a pre-orderable group is orderable, it is pre-orderable. There exist orderable groups which are not pre-orderable, but whose quotient groups by their centres are pre-orderable. The class of pre-orderable groups is closed with respect to direct products but not with respect to complete direct products, and is consequently non-axiomatizable (cf. Axiomatized class). A wreath product of pre-orderable groups is not always pre-orderable. A subgroup  of a group
of a group 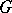 is said to be a
is said to be a 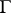 -pre-orderable group if any maximal partial order on
-pre-orderable group if any maximal partial order on 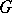 induces a total order on
induces a total order on  .
.
References
| [1] | A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian) |
| [2] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
Comments
In English the term "O*-group" is generally used in preference to "pre-orderable group" ; the latter is potentially misleading, because it suggests a (non-existent) connection with the notion of a pre-order.
Pre-orderable group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pre-orderable_group&oldid=13298