Postnikov square
From Encyclopedia of Mathematics
A cohomology operation of type 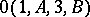 , where
, where 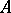 and
and 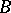 are Abelian groups with a fixed heteromorphism
are Abelian groups with a fixed heteromorphism  , i.e. a mapping such that the function
, i.e. a mapping such that the function
 |
is bilinear and 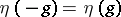 . Let
. Let 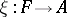 be an epimorphism and let
be an epimorphism and let 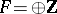 be a free Abelian group. The Postnikov square for
be a free Abelian group. The Postnikov square for  -cocycles is defined by the formula
-cocycles is defined by the formula
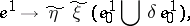 |
where 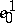 is a cochain with coefficients in
is a cochain with coefficients in 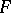 such that
such that 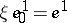 . A suspension of a Postnikov square is a Pontryagin square. For a simply-connected space
. A suspension of a Postnikov square is a Pontryagin square. For a simply-connected space 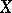 , the Postnikov square for which
, the Postnikov square for which 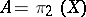 ,
, 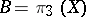 and
and 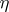 is defined by composition with the Hopf mapping
is defined by composition with the Hopf mapping 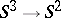 is used to classify the mappings of three-dimensional polyhedra into
is used to classify the mappings of three-dimensional polyhedra into 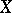 . Postnikov squares were introduced by M.M. Postnikov [1].
. Postnikov squares were introduced by M.M. Postnikov [1].
References
| [1] | M.M. Postnikov, "The classification of continuous mappings of a three-dimensional polyhedron into a simply connected polyhedron of arbitrary dimension" Dokl. Akad. Nauk SSSR , 64 : 4 (1949) pp. 461–462 (In Russian) |
How to Cite This Entry:
Postnikov square. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Postnikov_square&oldid=16646
Postnikov square. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Postnikov_square&oldid=16646
This article was adapted from an original article by A.F. Kharshiladze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article