Pontryagin square
A cohomology operation 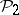 of type
of type 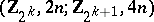 , i.e. a functorial mapping
, i.e. a functorial mapping
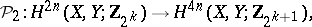 |
defined for any pair of topological spaces 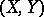 and such that for any continuous mapping
and such that for any continuous mapping 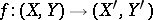 the equality
the equality 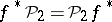 (naturality) holds.
(naturality) holds.
Pontryagin squares have the following properties:
1) 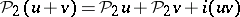 , where
, where 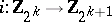 is the natural imbedding.
is the natural imbedding.
2) 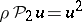 and
and 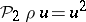 , where
, where 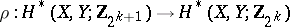 is the quotient homomorphism modulo
is the quotient homomorphism modulo 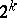 .
.
3)  , where
, where 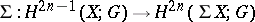 is the suspension mapping and
is the suspension mapping and 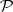 is the Postnikov square (in other words, the cohomology suspension of
is the Postnikov square (in other words, the cohomology suspension of 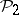 is
is 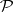 ). If
). If
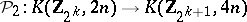 |
and
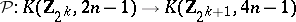 |
are the representing mappings, then 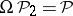 .
.
The properties 1), 2) uniquely characterize the Pontryagin square and thus can be taken as an axiomatic definition of it. Constructively the Pontryagin square is defined by the formula
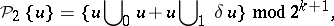 |
where 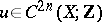 is a cocycle modulo
is a cocycle modulo 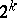 (for the
(for the 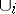 -products see Steenrod square).
-products see Steenrod square).
There exists (see [5], [6]) a generalization of the Pontryagin square to the case when 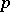 is an arbitrary odd prime number. This generalization is a cohomology operation of type
is an arbitrary odd prime number. This generalization is a cohomology operation of type 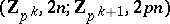 and is called the
and is called the 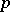 -th Pontryagin power
-th Pontryagin power 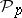 . The operation
. The operation 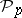 is uniquely defined by the following formulas:
is uniquely defined by the following formulas:
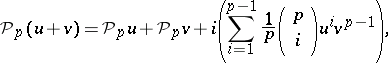 |
where 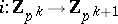 is the natural imbedding; and
is the natural imbedding; and
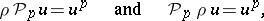 |
where 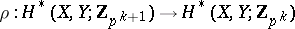 is the quotient homomorphism modulo
is the quotient homomorphism modulo 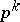 generalizing the corresponding formulas for
generalizing the corresponding formulas for 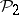 . The analogue of formula 3) for
. The analogue of formula 3) for 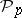 has the form
has the form 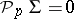 , which means that the cohomology suspension of
, which means that the cohomology suspension of 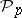 for
for 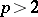 is zero. For
is zero. For 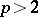 the equality
the equality 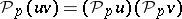 holds, the multiplication may be taken both as outer (
holds, the multiplication may be taken both as outer ( -multiplication) or inner (
-multiplication) or inner (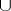 -multiplication). For
-multiplication). For 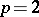 the corresponding equality is valid only up to summands of order 2.
the corresponding equality is valid only up to summands of order 2.
In the most general way the Pontryagin square is defined for cohomology with coefficients in an arbitrary finitely-generated Abelian group 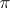 (see [2], [3]). In final form this generalization is as follows (see [6]). The Pontryagin square is a ring homomorphism
(see [2], [3]). In final form this generalization is as follows (see [6]). The Pontryagin square is a ring homomorphism
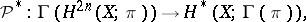 |
where 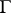 is a functor which associates a ring with divided powers to an Abelian group. For
is a functor which associates a ring with divided powers to an Abelian group. For 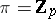 , the
, the 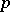 -th component of this homomorphism coincides with the
-th component of this homomorphism coincides with the 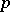 -th Pontryagin power
-th Pontryagin power 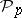 (for
(for 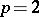 with the Pontryagin square
with the Pontryagin square 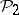 ).
).
References
| [1] | L.S. Pontryagin, "Mappings of a 3-dimensional sphere into an  -dimensional complex" Dokl. Akad. Nauk SSSR , 34 (1942) pp. 35–37 (In Russian) -dimensional complex" Dokl. Akad. Nauk SSSR , 34 (1942) pp. 35–37 (In Russian) |
| [2] | V.G. Boltyanskii, "The homotopy theory of continuous mapping and vector fields" , Moscow (1955) (In Russian) |
| [3] | M.M. Postnikov, "The classification of continuous mappings of a three-dimensional polyhedron into a simply connected polyhedron of arbitrary dimension" Dokl. Akad. Nauk SSSR , 64 : 4 (1949) pp. 461–462 (In Russian) |
| [4] | W. Browder, E. Thomas, "Axioms for the generalized Pontryagin cohomology operations" Quart. J. Math. , 13 (1962) pp. 55–60 |
| [5] | E. Thomas, "A generalization of the Pontrjagin square cohomology operation" Proc. Nat. Acad. Sci. USA , 42 (1956) pp. 266–269 |
| [6] | E. Thomas, "The generalized Pontryagin cohomology operations and rings with divided powers" , Amer. Math. Soc. (1957) |
Comments
For a definition of 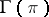 see Ring with divided powers.
see Ring with divided powers.
Pontryagin square. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pontryagin_square&oldid=17531