Difference between revisions of "Polygon (over a monoid)"
(→Comments: TeX partially done) |
(TeX partially done) |
||
| Line 1: | Line 1: | ||
| − | '' | + | ''$R$-polygon, operand'' |
| − | |||
| − | |||
| − | |||
| − | |||
| + | A non-empty set with a [[monoid]] of operators. More precisely, a non-empty set $A$ is called a left polygon over a monoid $R$ if for any $\lambda \in R$ and $a \in A$ the product $\lambda a \in A$ is defined, such that | ||
| + | $$ | ||
| + | \lambda (\mu a) = (\lambda\mu) a | ||
| + | $$ | ||
and | and | ||
| − | + | $$ | |
| − | + | 1a = a | |
| − | + | $$ | |
| − | for any | + | for any $\lambda, \mu \in R$, $a \in A$. A right polygon is defined similarly. Specifying an $R$-polygon $A$ is equivalent to specifying a homomorphism $\phi$ from the monoid $R$ into the monoid of mappings of the set $A$ into itself that transforms 1 to the identity mapping. Here $\lambda a = b$ if and only if |
| − | + | $$ | |
| − | + | \phi(\lambda)a = b$ \ . | |
| − | + | $$ | |
In particular, each non-empty set may be considered as a polygon over the monoid of its mappings into itself. Therefore, polygons are closely related to the representation of semi-groups by transformations: cf. [[Transformation semi-group]]. | In particular, each non-empty set may be considered as a polygon over the monoid of its mappings into itself. Therefore, polygons are closely related to the representation of semi-groups by transformations: cf. [[Transformation semi-group]]. | ||
| − | If | + | If $A$ is a [[universal algebra]] whose signature $\Omega$ contains only unary operations, then $A$ can be converted into a polygon over the free monoid $F$ generated by $\Omega$ by putting |
| − | + | $$ | |
| − | + | f_1 \cdots f_n a = f_1(\cdots(f_n(a)\cdots) | |
| + | $$ | ||
| − | for any | + | for any $f_i \in \Omega$, $a \in A$. If $\Omega$ is the set of input signals for an automaton having set of states $A$, then $A$ is similarly transformed into an $F$-polygon (cf. [[Automata, algebraic theory of]]). |
A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359032.png" /> of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359033.png" />-polygon <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359034.png" /> into an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359035.png" />-polygon <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359036.png" /> is called a homomorphism if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359037.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359038.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359039.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359040.png" /> one arrives at the definition of an endomorphism. All endomorphisms of a polygon <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359041.png" /> form a monoid, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359042.png" /> can be considered as a polygon over it. | A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359032.png" /> of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359033.png" />-polygon <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359034.png" /> into an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359035.png" />-polygon <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359036.png" /> is called a homomorphism if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359037.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359038.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359039.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359040.png" /> one arrives at the definition of an endomorphism. All endomorphisms of a polygon <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359041.png" /> form a monoid, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073590/p07359042.png" /> can be considered as a polygon over it. | ||
Revision as of 21:19, 19 December 2015
$R$-polygon, operand
A non-empty set with a monoid of operators. More precisely, a non-empty set $A$ is called a left polygon over a monoid $R$ if for any $\lambda \in R$ and $a \in A$ the product $\lambda a \in A$ is defined, such that $$ \lambda (\mu a) = (\lambda\mu) a $$ and $$ 1a = a $$ for any $\lambda, \mu \in R$, $a \in A$. A right polygon is defined similarly. Specifying an $R$-polygon $A$ is equivalent to specifying a homomorphism $\phi$ from the monoid $R$ into the monoid of mappings of the set $A$ into itself that transforms 1 to the identity mapping. Here $\lambda a = b$ if and only if $$ \phi(\lambda)a = b$ \ . $$ In particular, each non-empty set may be considered as a polygon over the monoid of its mappings into itself. Therefore, polygons are closely related to the representation of semi-groups by transformations: cf. Transformation semi-group.
If $A$ is a universal algebra whose signature $\Omega$ contains only unary operations, then $A$ can be converted into a polygon over the free monoid $F$ generated by $\Omega$ by putting $$ f_1 \cdots f_n a = f_1(\cdots(f_n(a)\cdots) $$
for any $f_i \in \Omega$, $a \in A$. If $\Omega$ is the set of input signals for an automaton having set of states $A$, then $A$ is similarly transformed into an $F$-polygon (cf. Automata, algebraic theory of).
A mapping 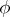 of an
of an 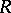 -polygon
-polygon 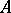 into an
into an 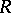 -polygon
-polygon 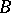 is called a homomorphism if
is called a homomorphism if 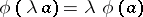 for any
for any 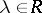 and
and 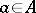 . For
. For  one arrives at the definition of an endomorphism. All endomorphisms of a polygon
one arrives at the definition of an endomorphism. All endomorphisms of a polygon 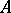 form a monoid, and
form a monoid, and 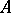 can be considered as a polygon over it.
can be considered as a polygon over it.
An equivalence  on an
on an 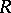 -polygon
-polygon 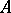 is called a congruence if
is called a congruence if 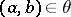 implies
implies 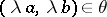 for any
for any 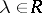 . The set of congruence classes of
. The set of congruence classes of 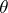 is naturally transformed into an
is naturally transformed into an 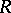 -polygon, called a quotient polygon of the polygon
-polygon, called a quotient polygon of the polygon 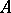 and denoted by
and denoted by  . If
. If  is a polygon over
is a polygon over 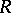 , then in
, then in  one can define a relation
one can define a relation 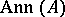 by putting
by putting 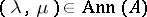 if
if 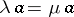 for all
for all 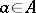 . The relation
. The relation  is a congruence on the monoid
is a congruence on the monoid 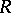 , and
, and 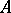 is transformed in a natural fashion into a polygon over the quotient monoid
is transformed in a natural fashion into a polygon over the quotient monoid 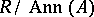 . If the polygon
. If the polygon 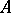 arose from a certain automaton, then this transition is equivalent to identifying identically acting sequences of input signals. In universal algebra one considers the usual constructions of direct and subdirect product, but in addition in polygon theory one may consider a wreath product construction important in the algebraic theory of automata. The free product (or co-product) of polygons coincides with their disjoint union.
arose from a certain automaton, then this transition is equivalent to identifying identically acting sequences of input signals. In universal algebra one considers the usual constructions of direct and subdirect product, but in addition in polygon theory one may consider a wreath product construction important in the algebraic theory of automata. The free product (or co-product) of polygons coincides with their disjoint union.
A polygon may be regarded as a non-additive analogue of a module over a ring, which serves as a rich source of problems in the theory of polygons. In particular, a relationship has been established between polygons and radicals in semi-groups (cf. Radical in a class of semi-groups), and studies have been made on the relation between the properties of a monoid and those of polygons over them. For example, all left  -polygons are projective if and only if
-polygons are projective if and only if  is a one-element group, while the injectivity of all polygons over a commutative monoid
is a one-element group, while the injectivity of all polygons over a commutative monoid 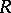 is equivalent to the presence in
is equivalent to the presence in  of a zero and the generation of all its ideals by idempotents (see Homological classification of rings).
of a zero and the generation of all its ideals by idempotents (see Homological classification of rings).
If 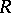 is a monoid with zero 0, one can speak of an
is a monoid with zero 0, one can speak of an 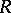 -polygon
-polygon 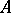 with a zero as an
with a zero as an 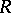 -polygon with a distinguished point
-polygon with a distinguished point  satisfying
satisfying 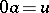 for all
for all 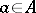 . The theory of polygons containing zeros has some special features.
. The theory of polygons containing zeros has some special features.
Every polygon can be considered as a functor from a one-object category into the category of sets.
References
| [1] | M.A. Arbib (ed.) , Algebraic theory of machines, languages and semigroups , Acad. Press (1968) |
| [2] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 2 , Amer. Math. Soc. (1967) |
| [3] | L.A. Skornyakov, "Generalizations of modules" , Modules , 3 , Novosibirsk (1973) pp. 22–27 (In Russian) |
| [4] | L.A. Skornyakov, A.V. Mikhalev, "Modules" Itogi Nauk. i Tekhn. Alg. Topol. Geom. , 14 (1976) pp. 57–190 (In Russian) |
Comments
In the West, left polygons over a monoid $M$ are usually called $M$-sets; the term "operand" is also in use. The category of all $M$-sets ($M$ fixed) forms a topos; but for this it is essential not to exclude (as above) the empty $M$-set.
Without assuming commutativity as above, the monoids all of whose non-empty left polygons (or, all of whose pointed left polygons) are injective have a few characterizations, which are reviewed in [a3]. As noted above, there are no non-trivial monoids all of whose left polygons are projective, but the perfect monoids, defined (like perfect rings, cf. Perfect ring) by every left polygon having a projective covering, are non-trivial; see [a1], [a2].
References
| [a1] | J. Fountain, "Perfect semigroups" Proc. Edinburgh Math. Soc. , 20 (1976) pp. 87–93 |
| [a2] | J. Isbell, "Perfect monoids" Semigroup Forum , 2 (1971) pp. 95–118 |
| [a3] | R.W. Yoh, "Congruence relations on left canonic semigroups" Semigroup Forum (1977) pp. 175–183 |
| [a4] | S. Eilenberg, "Automata, languages and machines" , Acad. Press (1974) |
Comments
The terms monoid action or monoid act, or action of a monoid on a set are also common, as is act for the set acted on; see [b1].
References
| [b1] | Mati Kilp, Ulrich Knauer, Alexander V. Mikhalev, Monoids, Acts and Categories: With Applications to Wreath Products and Graphs, Walter de Gruyter (2000) ISBN 3110812908 |
Polygon (over a monoid). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polygon_(over_a_monoid)&oldid=36988