Polycyclic group

A group possessing a polycyclic series, i.e. a subnormal series with cyclic factors (see Subgroup series). The class of polycyclic groups coincides with the class of solvable groups with the maximum condition for subgroups; it is closed under transition to subgroups, quotient groups and extensions. The number of infinite factors in any polycyclic series is an invariant of the polycyclic group (the polycyclic dimension). The holomorph of a polycyclic group (cf. Holomorph of a group) is isomorphic to a group of matrices over the ring of integers; this enables one to use methods from algebraic geometry, number theory and 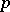-adic analysis in the theory of polycyclic groups. If 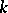is an algebraic extension of a finite field and 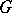is a finite extension of a polycyclic group, then any simple 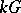-module is finite-dimensional over 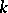. In any group, the product of two locally polycyclic normal subgroups is a locally polycyclic subgroup.

References

[1]	M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian)
[2]	B.A.F. Wehrfritz, "Three lectures on polycyclic groups" , Queen Mary College London (1973)

Comments

Every solvable linear group over the integers is polycyclic, [a1]. A solvable group is polycyclic if and only if every subgroup is finitely generated, [a2]. The Milnor–Wolf theorem says that a finitely-generated solvable group is either of polynomial or of exponential growth (cf. Polynomial and exponential growth in groups and algebras), and if it is of polynomial growth, then it is polycyclic and almost nilpotent (i.e. it contains a subgroup of finite index that is nilpotent) [a2], [a3]. If 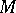is a complete, connected, locally homogeneous Riemannian manifold, then every solvable subgroup of its homotopy group 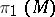is polycyclic, [a2].

The theorem that every polycyclic group is isomorphic to a matrix group over the integers was first proved in [a5]. The theorem that the polycyclic groups are precisely the solvable groups satisfying the maximum condition for subgroups comes from [a7].

References

[a1]	A.I. [A.I. Mal'tsev] Mal'Avcev, "On certain classes of infinite soluble groups" Transl. Amer. Math. Soc. (2) , 2 (1956) pp. 1–21 Mat. Sb. , 28 (1951) pp. 567–588
[a2]	J.A. Wolf, "Growth of finitely generated solvable groups and curvature of Riemannian manifolds" J. Diff. Geom. , 2 (1968) pp. 421–446
[a3]	J. Milnor, "Growth of finitely generated solvable groups" J. Diff. Geom. , 2 (1968) pp. 1–7
[a4]	D. Segal, "Polycyclic groups" , Cambridge Univ. Press (1983)
[a5]	L. Auslander, "On a problem of Philip Hall" Ann. of Math. , 86 (1967) pp. 112–116
[a6]	D. Segal, "The general polycyclic group" Bull. London Math. Soc. , 19 (1987) pp. 49–56
[a7]	K.A. Hirsch, "On infinite soluble groups" Proc. London Math. Soc. , 44 (1938) pp. 53–60