Polar coordinates

The numbers and (see ) related to rectangular Cartesian coordinates and by the formulas:

where , . The coordinate lines are: concentric circles ( ) and rays ().

Figure: p073410a

The system of polar coordinates is an orthogonal system. To each point in the -plane (except the point 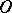for which and 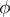is undefined, i.e. can be any number ) corresponds a pair of numbers and vice versa. The distance 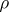between a point 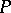and 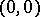(the pole) is called the polar radius, and the angle is called the polar angle. The Lamé coefficients (scale factors) are:

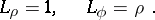The surface element is:

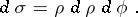The fundamental operations of vector analysis are:

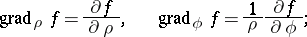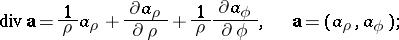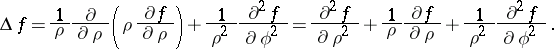The numbers and 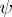related to Cartesian rectangular coordinates and by the formulas:

where 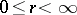, , 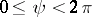, , 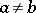are called generalized polar coordinates. The coordinate lines are: ellipses () and rays ().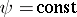

References

[1]	G.A. Korn, T.M. Korn, "Mathematical handbook for scientists and engineers" , McGraw-Hill (1961)

Comments

The generalization of polar coordinates to 3 dimensions are the spherical coordinates.

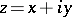By viewing a point as a complex number , the polar coordinates 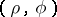correspond to the representation of as .

See also Complex number.

References

[a1]	H. Triebel, "Analysis and mathematical physics" , Reidel (1986) pp. 103
[a2]	K. Rektorys (ed.) , Applicable mathematics , Iliffe (1969) pp. 216