Polar
The polar of a point  with respect to a non-degenerate conic is the line containing all points harmonically conjugate to
with respect to a non-degenerate conic is the line containing all points harmonically conjugate to  with respect to the points
with respect to the points  and
and  of intersection of the conic with secants through
of intersection of the conic with secants through  (cf. Cross ratio). The point
(cf. Cross ratio). The point  is called the pole. If the point
is called the pole. If the point  lies outside the conic, then the polar passes through the points of contact of the two tangent lines that can be drawn through
lies outside the conic, then the polar passes through the points of contact of the two tangent lines that can be drawn through  (see Fig. a). If the point
(see Fig. a). If the point  lies on the curve, then the polar is the tangent to the curve at this point. If the polar of the point
lies on the curve, then the polar is the tangent to the curve at this point. If the polar of the point  passes through a point
passes through a point 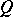 , then the polar of
, then the polar of 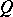 passes through
passes through 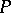 (see Fig. b).
(see Fig. b).

Figure: p073400a

Figure: p073400b
Every non-degenerate conic determines a bijection between the set of points of the projective plane and the set of its straight lines, which is a polarity (a polar transformation). Figures that correspond under this transformation are called mutually polar. A figure coinciding with its polar figure is called autopolar, or self-polar (see, for example, the self-polar triangle  in Fig. b).
in Fig. b).
Analogously one defines the polar (polar plane) of a point with respect to a non-degenerate surface of the second order.
The concept of a polar relative to a conic can be generalized to curves of order  . Here, a given point of the plane is put into correspondence with
. Here, a given point of the plane is put into correspondence with  polars with respect to the curve. The first of these polars is a curve of order
polars with respect to the curve. The first of these polars is a curve of order 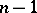 , the second, which is the polar of the given point relative to the first polar, has order
, the second, which is the polar of the given point relative to the first polar, has order  , etc., and, finally, the
, etc., and, finally, the  -st polar is a straight line.
-st polar is a straight line.
References
| [1] | N.V. Efimov, "Higher geometry" , MIR (1980) (Translated from Russian) |
| [2] | M.M. Postnikov, "Analytic geometry" , Moscow (1973) (In Russian) |
Comments
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a3] | H. Busemann, P.J. Kelly, "Projective geometry and projective metrics" , Acad. Press (1953) |
| [a4] | J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) pp. 195 |
The polar  of a subset
of a subset 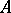 in a locally convex topological vector space
in a locally convex topological vector space 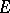 is the set of functionals
is the set of functionals  in the dual space
in the dual space  for which
for which 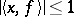 for all
for all  (here
(here  is the value of
is the value of  at
at  ). The bipolar
). The bipolar  is the set of vectors
is the set of vectors  in the space
in the space  for which
for which  for all
for all  .
.
The polar is convex, balanced and closed in the weak- topology
topology  . The bipolar
. The bipolar  is the weak closure of the convex balanced hull of the set
is the weak closure of the convex balanced hull of the set 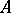 . In addition,
. In addition,  . If
. If  is a neighbourhood of zero in the space
is a neighbourhood of zero in the space  , then its polar
, then its polar  is a compactum in the weak-
is a compactum in the weak- topology (the Banach–Alaoglu theorem).
topology (the Banach–Alaoglu theorem).
The polar of the union  of any family
of any family  of sets in
of sets in  is the intersection of the polars of these sets. The polar of the intersection of weakly-closed convex balanced sets
is the intersection of the polars of these sets. The polar of the intersection of weakly-closed convex balanced sets  is the closure in the weak-
is the closure in the weak- topology of the convex hull of their polars. If
topology of the convex hull of their polars. If  is a subspace of
is a subspace of  , then its polar coincides with the subspace of
, then its polar coincides with the subspace of  orthogonal to
orthogonal to  .
.
As a fundamental system of neighbourhoods of zero defining the weak- topology of the space
topology of the space  one can take the system of sets of the form
one can take the system of sets of the form  where
where 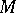 runs through all finite subsets of
runs through all finite subsets of  .
.
A subset of functionals of the space  is equicontinuous if and only if it is contained in the polar of some neighbourhood of zero.
is equicontinuous if and only if it is contained in the polar of some neighbourhood of zero.
References
| [1] | R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) |
V.I. Lomonosov
Comments
References
| [a1] | G. Köthe, "Topological vector spaces" , 1 , Springer (1979) (Translated from German) |
| [a2] | H.H. Schaefer, "Topological vector spaces" , Macmillan (1966) |
| [a3] | H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German) |
Polar. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polar&oldid=14444