Pointwise convergence

A type of convergence of sequences of functions (mappings). Let , where is some set and is a topological space; then pointwise convergence means that for any element the sequence of points , converges in the space . An important subclass of the pointwise-convergent sequences for the case of mappings between metric spaces (or, more generally, uniform spaces) is that of the uniformly-convergent sequences (cf. Uniform convergence).

Comments

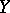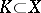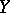A base for the topology of pointwise convergence on , the space of continuous mappings from to , is obtained as follows. Take a finite set and for each an open subset in containing 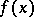; for a given 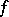an open basis neighbourhood is: 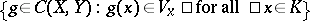. See also Pointwise convergence, topology of.

References

[a1]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) pp. 86 (Translated from Russian)