Point estimator
A statistical estimator whose values are points in the set of values of the quantity to be estimated.
Suppose that in the realization  of the random vector
of the random vector  , taking values in a sample space
, taking values in a sample space  ,
,  , the unknown parameter
, the unknown parameter  (or some function
(or some function  ) is to be estimated. Then any statistic
) is to be estimated. Then any statistic  producing a mapping of the set
producing a mapping of the set  into
into  (or into the set of values of
(or into the set of values of 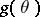 ) is called a point estimator of
) is called a point estimator of 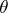 (or of the function
(or of the function 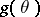 to be estimated). Important characteristics of a point estimator
to be estimated). Important characteristics of a point estimator 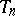 are its mathematical expectation
are its mathematical expectation
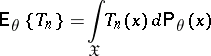 |
and the covariance matrix
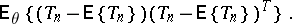 |
The vector 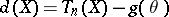 is called the error vector of the point estimator
is called the error vector of the point estimator 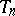 . If
. If
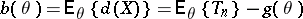 |
is the zero vector for all  , then one says that
, then one says that 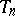 is an unbiased estimator of
is an unbiased estimator of 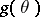 or that
or that 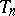 is free of systematic errors; otherwise,
is free of systematic errors; otherwise, 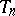 is said to be biased, and the vector
is said to be biased, and the vector  is called the bias or systematic error of the point estimator. The quality of a point estimator can be defined by means of the risk function (cf. Risk of a statistical procedure).
is called the bias or systematic error of the point estimator. The quality of a point estimator can be defined by means of the risk function (cf. Risk of a statistical procedure).
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | I.A. Ibragimov, R.Z. [R.Z. Khas'minskii] Has'minskii, "Statistical estimation: asymptotic theory" , Springer (1981) (Translated from Russian) |
Comments
References
| [a1] | E.L. Lehmann, "Theory of point estimation" , Wiley (1983) |
Point estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Point_estimator&oldid=16171