Poincaré model
Poincaré interpretation
A model realizing the geometry of the Lobachevskii plane (hyperbolic geometry) in the complex plane. In the Poincaré model with a circular absolute, every point of the unit disc  in the complex plane is called a hyperbolic point and the disc itself is called the hyperbolic plane. Circular arcs (and diameters) in
in the complex plane is called a hyperbolic point and the disc itself is called the hyperbolic plane. Circular arcs (and diameters) in  which are orthogonal to the boundary circle
which are orthogonal to the boundary circle  are called hyperbolic lines. Every point of
are called hyperbolic lines. Every point of  is called an ideal point. Hyperbolic lines with a common hyperbolic point are said to be intersecting lines; those with a common ideal point are called parallel; and those lines which do not intersect and are not parallel are called ultra-parallel (divergent). So, for example, in Fig. a two lines are depicted passing through the point
is called an ideal point. Hyperbolic lines with a common hyperbolic point are said to be intersecting lines; those with a common ideal point are called parallel; and those lines which do not intersect and are not parallel are called ultra-parallel (divergent). So, for example, in Fig. a two lines are depicted passing through the point  and both are parallel to the line
and both are parallel to the line 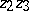 .
.

Figure: p073070a
In the Poincaré model in the half-plane  , every point of the upper half-plane is called a hyperbolic point and the half-plane itself is called the hyperbolic plane. Semi-circles and half-lines which are orthogonal to the real axis are called hyperbolic lines. The set of ideal points (the absolute) is the real axis together with the point at infinity of the
, every point of the upper half-plane is called a hyperbolic point and the half-plane itself is called the hyperbolic plane. Semi-circles and half-lines which are orthogonal to the real axis are called hyperbolic lines. The set of ideal points (the absolute) is the real axis together with the point at infinity of the  -plane. Parallel, intersecting and divergent lines are defined as in the Poincaré model with a circular absolute. So, for example, in Fig. b two lines passing through the point
-plane. Parallel, intersecting and divergent lines are defined as in the Poincaré model with a circular absolute. So, for example, in Fig. b two lines passing through the point  and parallel to the line
and parallel to the line 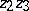 are depicted.
are depicted.

Figure: p073070b
The motions can be described as conformal transformations sending the absolute onto itself. Distance is defined using the cross ratio of four points:
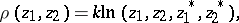 |
where 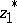 is the ideal point of the half-line emanating from
is the ideal point of the half-line emanating from  and passing through
and passing through 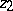 ,
, 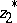 is the ideal point of the half-line emanating from
is the ideal point of the half-line emanating from 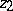 and passing through
and passing through 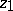 ,
,  is an arbitrary positive constant, and
is an arbitrary positive constant, and
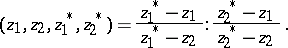 |
The angular measurements in the Poincaré model are the same as in hyperbolic geometry (cf. Lobachevskii geometry).
H. Poincaré (1882) proposed this model.
References
| [1] | F. Klein, "Elementary mathematics from a higher viewpoint" , Macmillan (1939) (Translated from German) |
| [2] | V.F. Kagan, "Lobachevskii and his geometry" , Moscow (1955) (In Russian) |
| [3] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
| [4] | H. Poincaré, "Oeuvres" , Gauthier-Villars (1916–1956) |
| [5] | R. Nevanlinna, "Uniformisierung" , Springer (1967) |
| [6] | G. Sansone, J. Gerretsen, "Lectures on the theory of functions of a complex variable" , 2. Geometric theory , Wolters-Noordhoff (1969) |
Comments
Alternatively, 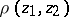 , being equal to the distance between hyperbolic lines through
, being equal to the distance between hyperbolic lines through 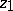 and
and 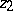 orthogonal to the line
orthogonal to the line 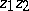 , can be defined as the inverse distance between the circles representing those two lines. (The inverse distance between two non-intersecting circles in the Euclidean plane is
, can be defined as the inverse distance between the circles representing those two lines. (The inverse distance between two non-intersecting circles in the Euclidean plane is 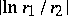 , where
, where 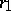 and
and 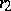 are the radii of any two concentric circles into which the given circles can be inverted.)
are the radii of any two concentric circles into which the given circles can be inverted.)
References
| [a1] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1969) pp. 90, 303 |
| [a2] | H.S.M. Coxeter, "Parallel lines" Canad. Math. Bull. , 21 (1978) pp. 385–397 |
| [a3] | H.S.M. Coxeter, S.L. Greitzer, "Geometry revisited" , Random House (1967) |
| [a4] | H.M.S. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1957) |
| [a5] | M.J. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974) |
Poincaré model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poincar%C3%A9_model&oldid=15317