Difference between revisions of "Pfaffian problem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Cartan, "Sur la théorie des systèmes en involution et ses applications à la relativité" ''Bull. Soc. Math. France'' , '''59''' (1931) pp. 88–118 {{MR|1504975}} {{ZBL|0002.26401}} {{ZBL|57.0551.02}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Cartan, "Leçons sur les invariants intégraux" , Hermann (1922) {{MR|0355764}} {{ZBL|48.0538.02}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.K. Rashevskii, "Geometric theory of partial differential equations" , Moscow-Leningrad (1947) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) {{MR|0193578}} {{ZBL|0129.13102}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.A. Griffiths, "Exterior differential systems and the calculus of variations" , Birkhäuser (1983) {{MR|0684663}} {{ZBL|0512.49003}} </TD></TR></table> |
| Line 85: | Line 85: | ||
The first Cartan–Kähler existence theorem is now as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530198.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530199.png" />-dimensional integral manifold of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530200.png" /> which defines a regular element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530201.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530202.png" />. Suppose that there is a submanifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530203.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530204.png" /> containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530205.png" /> and of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530206.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530207.png" />. Then locally around <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530208.png" /> there exists a unique integral manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530209.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530210.png" /> contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530211.png" />. | The first Cartan–Kähler existence theorem is now as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530198.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530199.png" />-dimensional integral manifold of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530200.png" /> which defines a regular element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530201.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530202.png" />. Suppose that there is a submanifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530203.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530204.png" /> containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530205.png" /> and of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530206.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530207.png" />. Then locally around <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530208.png" /> there exists a unique integral manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530209.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530210.png" /> contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530211.png" />. | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530212.png" />, the only possible choice (locally) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530213.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530214.png" /> itself, and there is a unique integral manifold of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530215.png" /> extending <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530216.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530217.png" /> there is | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530212.png" />, the only possible choice (locally) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530213.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530214.png" /> itself, and there is a unique integral manifold of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530215.png" /> extending <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530216.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530217.png" /> there is "one arbitrary function worth" freedom in choosing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530218.png" /> and one re-encounters the phenomenon that the solution of a partial differential equation may depend on arbitrary functions (such as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530219.png" /> with as solutions any function of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530220.png" />). The second Cartan–Kähler existence theorem, which is obtained by repeated application of the first, details the dependence on initial conditions and arbitrary functions. |
An immediate corollary of the first Cartan–Kähler existence theorem is as follows. Suppose one is given an integral element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530221.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530222.png" /> of the differential system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530223.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530224.png" /> which contains a regular integral element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530225.png" />. Then there exists (locally) an integral manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530226.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530227.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530228.png" />. | An immediate corollary of the first Cartan–Kähler existence theorem is as follows. Suppose one is given an integral element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530221.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530222.png" /> of the differential system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530223.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530224.png" /> which contains a regular integral element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530225.png" />. Then there exists (locally) an integral manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530226.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530227.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072530/p072530228.png" />. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) pp. Chapt. V, Appendix 3 (Translated from French) {{MR|0882548}} {{ZBL|0643.53002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Cartan, "Les systèmes différentielles extérieurs et leur applications géométriques" , Hermann (1945)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E. Cartan, "Sur l'intégration des systèmes d'équations aux différentielles totales" ''Ann. Sci. Ec. Norm. Sup.'' , '''18''' (1901) pp. 241–311 {{MR|}} {{ZBL|32.0351.04}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Kähler, "Einführung in die Theorie der Systeme von Differentialgleichungen" , Teubner (1934) {{MR|}} {{ZBL|0011.16103}} {{ZBL|60.0401.08}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Kuranishi, "Lectures on exterior differential systems" , Tata Inst. (1962)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J. Dieudonné, "Eléments d'analyse" , '''4''' , Gauthier-Villars (1977) pp. Chapt. XVIII, Sect. 13 {{MR|0467780}} {{ZBL|}} </TD></TR></table> |
Revision as of 17:00, 15 April 2012
The problem of describing the integral manifolds of maximal dimension for a Pfaffian system of Pfaffian equations
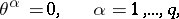 | (*) |
given by a collection of 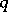 differential
differential 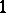 -forms which are linearly independent at each point in a certain domain
-forms which are linearly independent at each point in a certain domain 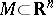 (or on a certain manifold). A submanifold
(or on a certain manifold). A submanifold 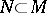 is called an integral manifold of the system (*) if the restrictions of the forms
is called an integral manifold of the system (*) if the restrictions of the forms 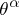 to
to 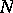 are identically zero. The problem was posed by J. Pfaff (1814).
are identically zero. The problem was posed by J. Pfaff (1814).
From a geometric point of view the system (*) determines an 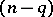 -dimensional distribution (a Pfaffian structure) on
-dimensional distribution (a Pfaffian structure) on 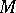 , that is, a field
, that is, a field
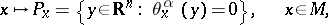 |
of 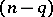 -dimensional subspaces, and the Pfaffian problem consists of describing the submanifolds of maximum possible dimension tangent to this field. The importance of the Pfaffian problem lies in the fact that the integration of an arbitrary partial differential equation can be reduced to a Pfaffian problem. For example, the integration of a first-order equation
-dimensional subspaces, and the Pfaffian problem consists of describing the submanifolds of maximum possible dimension tangent to this field. The importance of the Pfaffian problem lies in the fact that the integration of an arbitrary partial differential equation can be reduced to a Pfaffian problem. For example, the integration of a first-order equation
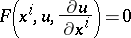 |
reduces to the Pfaffian problem for the Pfaffian equation 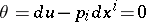 on the submanifold (generally speaking with singularities) of the space
on the submanifold (generally speaking with singularities) of the space 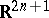 defined by the equation
defined by the equation
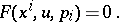 |
A completely-integrable Pfaffian system (and also a single Pfaffian equation of constant class) can be locally reduced to a simple canonical form. In these cases the solution of the Pfaffian problem reduces to the solution of ordinary differential equations. In the general case (in the class of smooth functions) the Pfaffian problem has not yet been solved (1989). The Pfaffian problem was solved by E. Cartan in the analytic case in his theory of systems in involution (cf. Involutional system). The formulation of the basic theorem of Cartan is based on the concept of a regular integral element. A  -dimensional subspace
-dimensional subspace 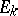 of the tangent space
of the tangent space 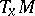 is called a
is called a 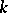 -dimensional integral element of the system (*) if
-dimensional integral element of the system (*) if
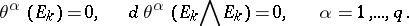 |
The subspace 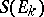 of the cotangent space
of the cotangent space 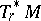 generated by the
generated by the 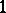 -forms
-forms 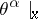 ,
, 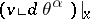 , where
, where  and
and  is the operation of interior multiplication (contraction), is called the polar system of the integral element
is the operation of interior multiplication (contraction), is called the polar system of the integral element 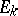 . The integral element
. The integral element 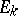 is regular if there exists a flag
is regular if there exists a flag 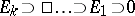 for which
for which
 |
where the maximum is taken over all 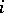 -dimensional integral elements
-dimensional integral elements 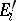 containing
containing 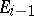 . Cartan's theorem asserts the following: Let
. Cartan's theorem asserts the following: Let 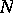 be a
be a 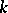 -dimensional integral manifold of a Pfaffian system with analytic coefficients and let, for a certain
-dimensional integral manifold of a Pfaffian system with analytic coefficients and let, for a certain 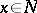 , the tangent space
, the tangent space 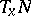 be a regular integral element. Then for any integral element
be a regular integral element. Then for any integral element 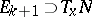 of dimension
of dimension 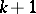 there exists in a certain neighbourhood of the point
there exists in a certain neighbourhood of the point  an integral manifold
an integral manifold 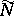 , locally containing
, locally containing 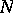 , for which
, for which 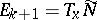 . Cartan's theorem has been generalized to arbitrary differential systems given by ideals in the algebra of differential forms on a manifold (the Cartan–Kähler theorem).
. Cartan's theorem has been generalized to arbitrary differential systems given by ideals in the algebra of differential forms on a manifold (the Cartan–Kähler theorem).
References
| [1] | E. Cartan, "Sur la théorie des systèmes en involution et ses applications à la relativité" Bull. Soc. Math. France , 59 (1931) pp. 88–118 MR1504975 Zbl 0002.26401 Zbl 57.0551.02 |
| [2] | E. Cartan, "Leçons sur les invariants intégraux" , Hermann (1922) MR0355764 Zbl 48.0538.02 |
| [3] | P.K. Rashevskii, "Geometric theory of partial differential equations" , Moscow-Leningrad (1947) (In Russian) |
| [4] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) MR0193578 Zbl 0129.13102 |
| [5] | P.A. Griffiths, "Exterior differential systems and the calculus of variations" , Birkhäuser (1983) MR0684663 Zbl 0512.49003 |
Comments
Pfaffian problems and partial differential equations.
Let
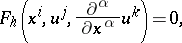 | (a1) |
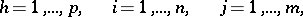 |
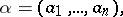 |
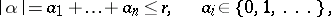 |
be a system 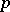 partial differential equations for
partial differential equations for  functions in
functions in  variables of order
variables of order 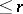 . Introduce the variables
. Introduce the variables
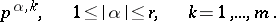 |
Replacing the equations (a1) with the equations
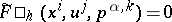 | (a2) |
and adding to this the Pfaffian system
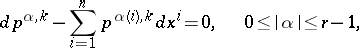 | (a3) |
where 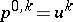 and
and  if
if 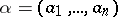 for
for 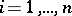 , one finds a system (a2)–(a3) of equations which are equivalent to equations (a1) in a suitable sense. Thus, if (locally) (a2) defines a subvariety
, one finds a system (a2)–(a3) of equations which are equivalent to equations (a1) in a suitable sense. Thus, if (locally) (a2) defines a subvariety 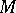 in
in 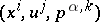 -space, then a solution of the Pfaffian problem (a3) on
-space, then a solution of the Pfaffian problem (a3) on 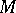 defines a solution of (a1) in the sense that the projection onto
defines a solution of (a1) in the sense that the projection onto 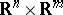 (or
(or 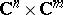 as the case may be) gives the graph of a solution of (a1).
as the case may be) gives the graph of a solution of (a1).
For instance, in the case of a single second-order equation
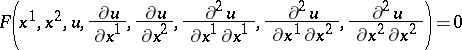 |
one has for (a2) and (a3), respectively,
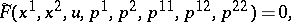 | (a2prm) |
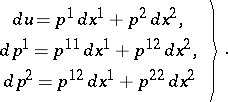 | (a3prm) |
The main equations are (a2); the remaining equations (a3) express that the solutions of (a2) of interest are  -jets (cf. Jet and Partial differential equations on a manifold) of functions
-jets (cf. Jet and Partial differential equations on a manifold) of functions 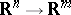 . This leads to the idea of a system of partial differential equations on a manifold of order
. This leads to the idea of a system of partial differential equations on a manifold of order  as being determined by a set of functions on the
as being determined by a set of functions on the  -th jet bundle; cf. Partial differential equations on a manifold for more details.
-th jet bundle; cf. Partial differential equations on a manifold for more details.
In the setting of equations like (a2), (a3) the following generalization of Frobenius' theorem on complete integrability is of interest. Let 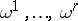 be a set of differential forms on a manifold
be a set of differential forms on a manifold 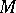 and
and 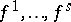 a set of functions on
a set of functions on 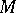 . Let
. Let 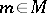 be such that
be such that 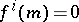 ,
, 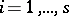 . Suppose that
. Suppose that
i) 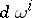 and
and 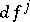 are in the ideal of differential forms generated by
are in the ideal of differential forms generated by 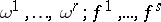 ;
;
ii) the 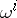 are linearly independent at
are linearly independent at 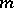 .
.
(Recall that the linearly independent 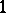 -forms
-forms 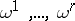 form an involutive system if
form an involutive system if 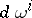 is in the ideal generated by the
is in the ideal generated by the 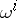 , cf. Involutive distribution.) Then there is a unique germ of a submanifold
, cf. Involutive distribution.) Then there is a unique germ of a submanifold 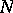 at
at 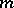 of dimension
of dimension  ,
, 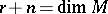 , such that the differential forms
, such that the differential forms 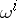 and functions
and functions  restricted to
restricted to 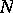 are zero. Further if
are zero. Further if  are functions on
are functions on 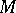 near
near 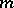 such that
such that 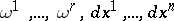 are linearly independent at
are linearly independent at 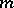 , then the
, then the  give a coordinate chart of
give a coordinate chart of  near
near 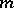 .
.
Cartan–Kähler theorem for differential systems defined by ideals.
Let 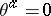 ,
, 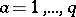 , be a Pfaffian system on
, be a Pfaffian system on 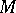 and let
and let 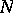 be an integral manifold of this system. Then obviously the
be an integral manifold of this system. Then obviously the 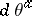 and
and 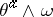 , where
, where 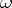 is any differential form on
is any differential form on 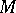 , are also zero on
, are also zero on 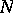 . Thus all the elements of the differential ideal generated by
. Thus all the elements of the differential ideal generated by 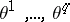 in the differential algebra of exterior differential forms
in the differential algebra of exterior differential forms 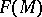 (cf. Differential form; Differential ring) are zero on
(cf. Differential form; Differential ring) are zero on 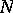 . This leads to the idea of a differential system (of equations) on
. This leads to the idea of a differential system (of equations) on 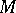 as being defined by such an ideal. From now on let
as being defined by such an ideal. From now on let 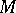 be a real analytic manifold. Let
be a real analytic manifold. Let 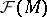 be the associated sheaf to
be the associated sheaf to 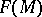 , i.e.
, i.e.  is the sheaf of germs of rings of differential forms on
is the sheaf of germs of rings of differential forms on 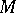 . Let
. Let 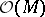 be the sheaf of analytic functions on
be the sheaf of analytic functions on 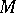 and let
and let 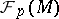 be the
be the  -module of
-module of 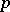 -forms on
-forms on 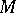 . A differential system on
. A differential system on 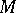 is a graded differential subsheaf
is a graded differential subsheaf 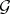 of ideals of
of ideals of 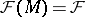 , i.e.
, i.e. 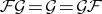 (the ideal property),
(the ideal property), 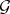 is generated by the
is generated by the 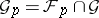 (the graded property) and
(the graded property) and 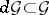 (the differential property). A
(the differential property). A 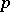 -dimensional integral manifold for
-dimensional integral manifold for 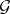 is a submanifold
is a submanifold 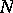 of
of 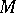 on which
on which 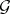 is zero. For each
is zero. For each 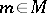 let
let 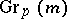 be the Grassmann manifold of
be the Grassmann manifold of 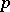 -dimensional subspaces of the tangent space
-dimensional subspaces of the tangent space 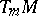 . The union of the
. The union of the 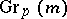 for
for 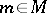 has a natural structure of a real-analytic manifold and the projection
has a natural structure of a real-analytic manifold and the projection 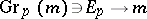 then defines a locally trivial fibre bundle
then defines a locally trivial fibre bundle 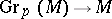 . An element
. An element 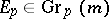 is called a contact element at
is called a contact element at 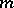 . Such an element is an integral element of
. Such an element is an integral element of 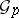 if
if 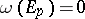 for all
for all 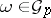 ; it is an integral element of a differential system
; it is an integral element of a differential system 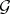 if for all
if for all 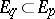 ,
, 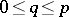 ,
,  is an integral element of
is an integral element of 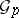 . An integral element of dimension zero (i.e. a point of
. An integral element of dimension zero (i.e. a point of 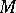 ) is an integral point (which is simply a solution of the equations
) is an integral point (which is simply a solution of the equations 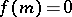 for the functions
for the functions 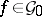 ). The polar element of an integral element
). The polar element of an integral element 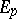 for
for 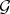 is the element
is the element 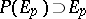 consisting of all vectors
consisting of all vectors 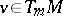 such that the span of
such that the span of 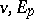 is an integral element of
is an integral element of 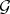 . Let
. Let 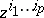 ,
, 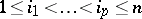 , be the Grassmann coordinates of
, be the Grassmann coordinates of 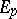 (cf. Exterior algebra; these are only defined up to a common scalar multiple). Now associate to
(cf. Exterior algebra; these are only defined up to a common scalar multiple). Now associate to 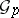 the sheaf
the sheaf 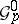 of
of 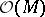 -modules in
-modules in 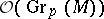 consisting of all the functions
consisting of all the functions 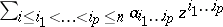 for all
for all 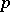 -forms
-forms 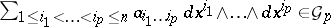 . Let
. Let  be the set of integral elements of
be the set of integral elements of 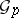 (so that
(so that 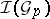 is a certain subset of the Grassmann bundle
is a certain subset of the Grassmann bundle 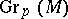 ). The element
). The element 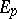 is called a regular integral element if
is called a regular integral element if 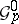 is a regular local equation for
is a regular local equation for 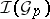 at
at 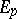 and
and 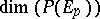 is constant near
is constant near 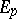 on
on 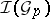 . Recall that a subsheaf
. Recall that a subsheaf 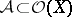 , where
, where 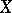 is a manifold, is a regular local equation for (its set of zeros)
is a manifold, is a regular local equation for (its set of zeros) 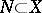 at
at 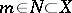 if locally around
if locally around 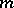 there exist sections
there exist sections 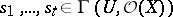 such that the
such that the 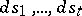 are linearly independent on
are linearly independent on 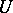 and
and 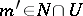 if and only if
if and only if 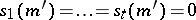 .
.
The first Cartan–Kähler existence theorem is now as follows. Let 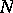 be a
be a 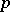 -dimensional integral manifold of
-dimensional integral manifold of 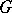 which defines a regular element
which defines a regular element 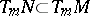 at
at 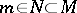 . Suppose that there is a submanifold
. Suppose that there is a submanifold 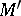 of
of 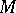 containing
containing 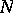 and of dimension
and of dimension 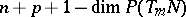 such that
such that 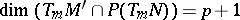 . Then locally around
. Then locally around 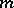 there exists a unique integral manifold
there exists a unique integral manifold 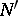 of dimension
of dimension 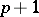 contained in
contained in 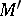 .
.
If 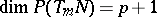 , the only possible choice (locally) for
, the only possible choice (locally) for 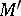 is
is 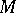 itself, and there is a unique integral manifold of dimension
itself, and there is a unique integral manifold of dimension 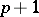 extending
extending 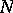 . If
. If 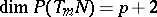 there is "one arbitrary function worth" freedom in choosing
there is "one arbitrary function worth" freedom in choosing 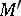 and one re-encounters the phenomenon that the solution of a partial differential equation may depend on arbitrary functions (such as
and one re-encounters the phenomenon that the solution of a partial differential equation may depend on arbitrary functions (such as 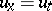 with as solutions any function of the form
with as solutions any function of the form 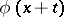 ). The second Cartan–Kähler existence theorem, which is obtained by repeated application of the first, details the dependence on initial conditions and arbitrary functions.
). The second Cartan–Kähler existence theorem, which is obtained by repeated application of the first, details the dependence on initial conditions and arbitrary functions.
An immediate corollary of the first Cartan–Kähler existence theorem is as follows. Suppose one is given an integral element 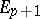 of dimension
of dimension 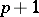 of the differential system
of the differential system 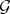 at
at 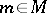 which contains a regular integral element
which contains a regular integral element 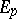 . Then there exists (locally) an integral manifold
. Then there exists (locally) an integral manifold 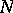 of dimension
of dimension 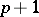 such that
such that 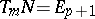 .
.
References
| [a1] | P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) pp. Chapt. V, Appendix 3 (Translated from French) MR0882548 Zbl 0643.53002 |
| [a2] | E. Cartan, "Les systèmes différentielles extérieurs et leur applications géométriques" , Hermann (1945) |
| [a3] | E. Cartan, "Sur l'intégration des systèmes d'équations aux différentielles totales" Ann. Sci. Ec. Norm. Sup. , 18 (1901) pp. 241–311 Zbl 32.0351.04 |
| [a4] | E. Kähler, "Einführung in die Theorie der Systeme von Differentialgleichungen" , Teubner (1934) Zbl 0011.16103 Zbl 60.0401.08 |
| [a5] | M. Kuranishi, "Lectures on exterior differential systems" , Tata Inst. (1962) |
| [a6] | J. Dieudonné, "Eléments d'analyse" , 4 , Gauthier-Villars (1977) pp. Chapt. XVIII, Sect. 13 MR0467780 |
Pfaffian problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pfaffian_problem&oldid=14825