Perron method
A method for solving the Dirichlet problem for the Laplace equation based on the properties of subharmonic functions (and superharmonic functions, cf. Subharmonic function). O. Perron [1] gave the initial presentation of the method, which was substantially developed by N. Wiener
and M.V. Keldysh [4].
Let  be a bounded domain in a Euclidean space
be a bounded domain in a Euclidean space 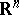 ,
, 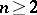 , with boundary
, with boundary 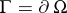 , let
, let 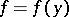 be a real-valued function on
be a real-valued function on 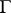 ,
, 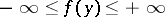 . Let
. Let 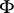 be the non-empty family of all superharmonic functions
be the non-empty family of all superharmonic functions 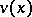 ,
, 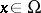 , in the wide sense (i.e. the function
, in the wide sense (i.e. the function  belongs to
belongs to 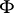 ) that are bounded from below and are such that
) that are bounded from below and are such that
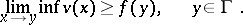 |
Let
 |
be the lower envelope of 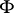 . Along with
. Along with 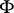 , consider the non-empty family
, consider the non-empty family 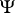 of all subharmonic functions
of all subharmonic functions 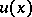 ,
, 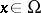 , in the wide sense (the function
, in the wide sense (the function 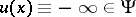 ) that are bounded from above and are such that
) that are bounded from above and are such that
 |
Let
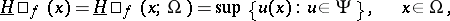 |
be the upper envelope of 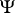 .
.
There are only three possibilities for 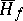 (and
(and 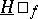 ):
): 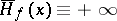 ,
, 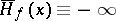 or
or 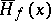 is a harmonic function; and always
is a harmonic function; and always
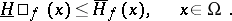 |
The function 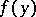 ,
, 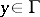 , is called resolutive if the two envelopes
, is called resolutive if the two envelopes 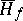 and
and 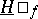 are finite and coincide. In that case the harmonic function
are finite and coincide. In that case the harmonic function  is the generalized solution to the Dirichlet problem for the function
is the generalized solution to the Dirichlet problem for the function 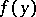 ,
, 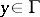 (in the sense of Wiener–Perron). For
(in the sense of Wiener–Perron). For 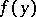 ,
, 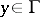 , to be resolutive it is necessary and sufficient that it be integrable with respect to the harmonic measure on
, to be resolutive it is necessary and sufficient that it be integrable with respect to the harmonic measure on 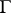 (Brelot's theorem). Any continuous finite function
(Brelot's theorem). Any continuous finite function 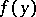 ,
, 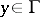 , is resolutive (Wiener's theorem).
, is resolutive (Wiener's theorem).
A point 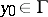 is called a regular boundary point if the following limit relation applies for any continuous finite function
is called a regular boundary point if the following limit relation applies for any continuous finite function 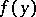 ,
, 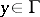 :
:
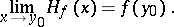 |
Regularity at all points 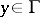 is equivalent to the existence of classical solutions
is equivalent to the existence of classical solutions 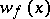 to the Dirichlet problem for any continuous finite function
to the Dirichlet problem for any continuous finite function 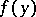 ,
, 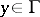 , and in that case
, and in that case 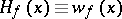 ; a bounded domain
; a bounded domain  all boundary points of which are regular is sometimes also called regular. For a point
all boundary points of which are regular is sometimes also called regular. For a point 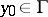 to be regular it is necessary and sufficient that there is a barrier at
to be regular it is necessary and sufficient that there is a barrier at  .
.
Points 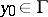 that are not regular are called irregular boundary points. For example, isolated points are irregular boundary points, as are the vertices of sufficiently sharp wedges entering
that are not regular are called irregular boundary points. For example, isolated points are irregular boundary points, as are the vertices of sufficiently sharp wedges entering  if
if 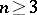 (Lebesgue spines). The set of all irregular points of
(Lebesgue spines). The set of all irregular points of  is a set of type
is a set of type 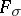 of capacity zero.
of capacity zero.
Let there be a sequence of domains 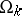 ,
,  , such that
, such that 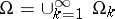 , and let a continuous finite function
, and let a continuous finite function 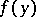 ,
, 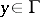 , be continuously extendible to
, be continuously extendible to 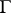 . Then
. Then
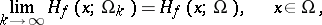 |
uniformly on compact sets in  ; in the case of regular domains
; in the case of regular domains 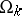 one obtains a construction à la Wiener for the generalized solution to the Dirichlet problem. Now consider an arbitrary sequence of domains
one obtains a construction à la Wiener for the generalized solution to the Dirichlet problem. Now consider an arbitrary sequence of domains 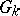 ,
, 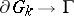 ,
, 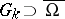 , for a domain
, for a domain  without an interior boundary. In that case, in general
without an interior boundary. In that case, in general
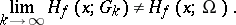 |
The Dirichlet problem is stable in a domain  or in a closed domain
or in a closed domain  if
if
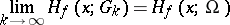 |
for all 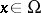 or for all
or for all 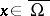 , respectively. For the Dirichlet problem to be stable in a domain
, respectively. For the Dirichlet problem to be stable in a domain  it is necessary and sufficient that the sets of all irregular points in the complements
it is necessary and sufficient that the sets of all irregular points in the complements 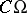 and
and 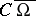 coincide; stability in a closed domain requires that
coincide; stability in a closed domain requires that 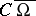 does not have irregular points (Keldysh' theorems, cf. Keldysh theorem and [4], where an example is also constructed of a regular domain
does not have irregular points (Keldysh' theorems, cf. Keldysh theorem and [4], where an example is also constructed of a regular domain  within which the Dirichlet problem is unstable).
within which the Dirichlet problem is unstable).
See also Upper-and-lower-functions method.
References
| [1] | O. Perron, "Eine neue Behandlung der ersten Randwertaufgabe für 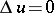 " Math. Z. , 18 (1923) pp. 42–54 " Math. Z. , 18 (1923) pp. 42–54 |
| [2] | I.G. Petrovskii, "Perron's method for the solution of the Dirichlet problem" Uspekhi Mat. Nauk , 8 (1941) pp. 107–114 (In Russian) |
| [3a] | N. Wiener, "Certain notions in potential theory" J. Math. Phys. , 3 (1924) pp. 24–51 |
| [3b] | N. Wiener, "The Dirichlet problem" J. Math. Phys. , 3 (1924) pp. 127–146 |
| [3c] | N. Wiener, "Note on paper of O. Perron" J. Math. Phys. , 4 (1925) pp. 21–32 |
| [4] | M.V. Keldysh, "On the solvability and stability of the Dirichlet problem" Uspekhi Mat. Nauk , 8 (1941) pp. 171–231 (In Russian) |
| [5] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
Comments
Counterexamples from S. Zaremba [a5] and H. Lebesgue [a2] made it clear that the existence of a classical solution to the Dirichlet problem for the Laplace equation is not always guaranteed. Lebesgue [a3] therefore proposed to construct a solution operator from the space of boundary functions into the set of harmonic functions on the domain. This operator should be linear and isotone (cf. Isotone mapping), and produce the classical solution if one exists. N. Wiener [3c] showed that such a solution operator for continuous boundary functions is obtained from the Perron method. The method is extended to arbitrary boundary functions by M. Brelot, and, since then, is called the Perron–Wiener–Brelot method. The uniqueness of the solution operator is proved by M.V. Keldysh (cf. Keldysh theorem). All these results have their counterpart in the abstract theory of harmonic spaces (cf. Harmonic space), cf. [a4].
References
| [a1] | M. Brelot, "Familles de Perron et problème de Dirichlet" Acta Sci. Math. (Szeged) , 9 (1938–1940) pp. 133–153 |
| [a2] | H. Lebesgue, "Sur des cas d'impossibilité du problème de Dirichlet ordinaire" C.R. Séances Soc. Math. France , 41 (1913) pp. 17 |
| [a3] | H. Lebesgue, "Conditions de régularité, conditions d'irrégularité, conditions d'impossibilité dans le problème de Dirichlet" C.R. Acad. Sci. , 178 (1924) pp. 349–354 |
| [a4] | I. Netuka, "The Dirichlet problem for harmonic functions" Amer. Math. Monthly , 87 (1980) pp. 621–628 |
| [a5] | S. Zaremba, "Sur le principe de Dirichlet" Acta Math. , 34 (1911) pp. 293–316 |
Perron method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perron_method&oldid=14033