Perfect ring
left
An associative ring such that every left module over it has a projective covering (cf. Associative rings and algebras). Right perfect rings are defined similarly. A left perfect ring need not be right perfect.
The following properties of a ring 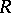 are equivalent: 1)
are equivalent: 1) 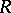 is a left perfect ring; 2) every set of pairwise orthogonal idempotents of
is a left perfect ring; 2) every set of pairwise orthogonal idempotents of 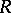 is finite, and every non-zero right
is finite, and every non-zero right 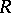 -module has a non-zero socle; 3)
-module has a non-zero socle; 3) 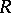 satisfies the minimum condition for principal right ideals; 4)
satisfies the minimum condition for principal right ideals; 4) 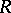 satisfies the minimum condition for finitely-generated right ideals; 5) every right
satisfies the minimum condition for finitely-generated right ideals; 5) every right 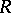 -module satisfies the minimum condition for finitely-generated submodules; 6) the Jacobson radical
-module satisfies the minimum condition for finitely-generated submodules; 6) the Jacobson radical  of
of  vanishes on the right (that is, for any sequence
vanishes on the right (that is, for any sequence 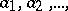 of elements of
of elements of 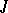 there is an integer
there is an integer  such that the product
such that the product 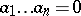 ), and the quotient ring
), and the quotient ring 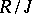 is Artinian semi-simple; 7) every flat left
is Artinian semi-simple; 7) every flat left 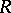 -module is projective; 8)
-module is projective; 8) 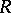 contains idempotents
contains idempotents  such that
such that 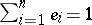 ,
,  for
for 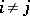 , and
, and  is a local ring for every
is a local ring for every 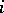 ; 9) every left
; 9) every left  -module satisfies the maximum condition for cyclic submodules; 10) for every
-module satisfies the maximum condition for cyclic submodules; 10) for every  every left
every left 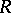 -module satisfies the maximum condition for
-module satisfies the maximum condition for  -generated submodules; and 11) every projective left
-generated submodules; and 11) every projective left 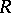 -module has a decomposition with respect to which every direct summand has a complement (see Krull–Remak–Schmidt theorem).
-module has a decomposition with respect to which every direct summand has a complement (see Krull–Remak–Schmidt theorem).
A ring of matrices over a perfect ring is perfect. Idempotent ideals of a perfect ring are generated by idempotents that are central modulo the radical. A group ring 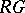 (see Group algebra) is perfect if and only if
(see Group algebra) is perfect if and only if  is a perfect ring and
is a perfect ring and 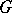 is a finite group. The endomorphism ring of an Abelian group
is a finite group. The endomorphism ring of an Abelian group 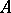 is perfect only when
is perfect only when 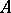 is the direct sum of a finite group and finitely many copies of the additive group of rational numbers. Local perfect rings are characterized by the fact that any linearly independent subset of any free left module over it can be extended to a base. The following properties are also equivalent: a)
is the direct sum of a finite group and finitely many copies of the additive group of rational numbers. Local perfect rings are characterized by the fact that any linearly independent subset of any free left module over it can be extended to a base. The following properties are also equivalent: a) 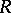 is a perfect ring and all its quotient rings are self-injective (cf. Self-injective ring); b) every quotient ring of
is a perfect ring and all its quotient rings are self-injective (cf. Self-injective ring); b) every quotient ring of 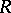 is quasi-Frobenius (cf. Quasi-Frobenius ring); c) every quotient ring of
is quasi-Frobenius (cf. Quasi-Frobenius ring); c) every quotient ring of 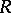 has a cogenerator; and d)
has a cogenerator; and d) 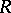 is uniserial (cf. Uniserial ring).
is uniserial (cf. Uniserial ring).
References
| [1] | F. Kasch, "Modules and rings" , Acad. Press (1982) (Translated from German) |
| [2] | C. Faith, "Algebra" , 1–2 , Springer (1973–1979) |
| [3] | V.T. Markov, A.V. Mikhalev, L.A. Skornyakov, A.A. Tuganbaev, "Modules" J. Soviet Math. , 23 : 6 (10983) pp. 2642–2706 Itogi Nauk. Algebra. Topol. Geom. , 19 (1981) pp. 31–134 |
Perfect ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perfect_ring&oldid=12697