Perfect number
A positive integer with the property that it coincides with the sum of all its positive divisors other than the number itself.
Thus, an integer 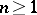 is a perfect number if
is a perfect number if
 |
For example, the numbers 6, 28, 496, 8128, 33550336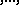 are perfect.
are perfect.
Perfect numbers are closely connected with Mersenne primes (see Mersenne number), i.e. prime numbers of the form  . Euclid already established that the number
. Euclid already established that the number
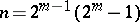 |
is perfect if 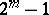 is a prime number. L. Euler showed that these exhaust all even perfect numbers.
is a prime number. L. Euler showed that these exhaust all even perfect numbers.
It is still (1983) unknown whether the set of even perfect numbers is finite or infinite, that is, it is unknown whether the set of Mersenne primes 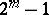 is finite or not. It is also unknown whether or not there are any odd perfect numbers.
is finite or not. It is also unknown whether or not there are any odd perfect numbers.
Twenty-seven even perfect numbers have been found up till now (1983). The first twenty-three of them correspond to the following values of 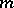 : 2, 3, 5, 7, 13, 17, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, and 11213. A list of perfect numbers from the twelfth to the twenty-fourth is given in [2]. The even numbers from the twenty-fifth to the twenty-seventh correspond to the following values of
: 2, 3, 5, 7, 13, 17, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, and 11213. A list of perfect numbers from the twelfth to the twenty-fourth is given in [2]. The even numbers from the twenty-fifth to the twenty-seventh correspond to the following values of 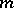 : 21701, 23209 and 44497 (see [3]). It has been shown (see [4]) that there are no odd perfect numbers in the interval from 1 to
: 21701, 23209 and 44497 (see [3]). It has been shown (see [4]) that there are no odd perfect numbers in the interval from 1 to  .
.
References
| [1] | L.E. Dickson, "History of the theory of numbers" , 1 , Chelsea, reprint (1952) |
| [2] | M.L. Nankar, "History of perfect numbers" Ganita Bharati , 1 : 1–2 (1979) pp. 7–8 |
| [3] | D. Slowinski, "Searching for the 27th Mersenne prime" J. Recreational Math. , 11 (1979) pp. 258–261 |
| [4] | P. Hagis, "A lower bound for the set of odd perfect prime numbers" Math. Comp. , 27 (1973) pp. 951–953 |
Comments
For a short history of perfect numbers see [a1]. It is still (1990) unknown whether the set of even perfect numbers if finite or infinite, but in the years 1983–1986 three more of them have been found. The values of 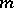 for the 24th to the 30th are: 19937, 21701, 23209, 44497, 86243, 132049 (see [a2]), and 216091 (1985).
for the 24th to the 30th are: 19937, 21701, 23209, 44497, 86243, 132049 (see [a2]), and 216091 (1985).
References
| [a1] | H.J.J. te Riele, "Perfect numbers and aliquot sequences" H.W. Lenstra (ed.) R. Tijdeman (ed.) , Computational Methods in Number Theory , 154 , CWI (1982) pp. 141–157 |
| [a2] | H. Riesel, "Prime numbers and computer methods for factorisation" , Birkhäuser (1985) |
Perfect number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perfect_number&oldid=15832