Penalty functions, method of
A method for reducing constrained extremum problems to problems of unconstrained optimization. The method of penalty functions may be illustrated for problems in mathematical programming. Consider the problem of minimizing a function  on a set
on a set 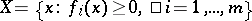 in an
in an  -dimensional Euclidean space. A penalty function, or penalty (for violating the restrictions
-dimensional Euclidean space. A penalty function, or penalty (for violating the restrictions 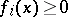 ,
, 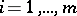 ), is a function
), is a function 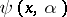 depending on
depending on  and a numerical parameter
and a numerical parameter  with the following properties:
with the following properties: 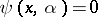 if
if 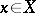 and
and 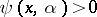 if
if 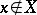 . Let
. Let 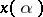 be any point where the function
be any point where the function 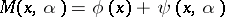 takes an unconstrained (global) minimum, and let
takes an unconstrained (global) minimum, and let 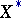 be the set of solutions of the original problem. The function
be the set of solutions of the original problem. The function 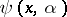 is chosen such that the distance between the points
is chosen such that the distance between the points 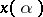 and the set
and the set  tends to zero for
tends to zero for 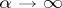 , or, if it is not possible to ensure this condition, such that the following relation holds:
, or, if it is not possible to ensure this condition, such that the following relation holds:
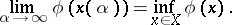 |
For  one often chooses the function
one often chooses the function
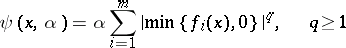 |
(frequently  ).
).
The choice of a particular form for the function 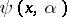 is connected both with the problem of convergence of the method of penalty functions, and with problems arising in the unconstrained minimization of
is connected both with the problem of convergence of the method of penalty functions, and with problems arising in the unconstrained minimization of 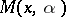 .
.
A more general statement of the method of penalty functions is based on reducing the problem of minimization of 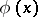 on a set
on a set  to the problem of minimizing some parametric function
to the problem of minimizing some parametric function  on a set of simpler structure (from the point of view of efficiency of applying numerical minimization methods) than the initial set
on a set of simpler structure (from the point of view of efficiency of applying numerical minimization methods) than the initial set 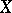 .
.
The following well-known general result shows that the method of penalty functions is universal. Let 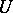 and
and 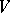 be reflexive Banach spaces (cf. Reflexive space); let
be reflexive Banach spaces (cf. Reflexive space); let  be the extended real line; let
be the extended real line; let 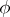 be a function defined on
be a function defined on 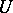 with values in
with values in 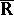 that is weakly lower semi-continuous (cf. Semi-continuous function); let
that is weakly lower semi-continuous (cf. Semi-continuous function); let 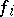 ,
, 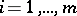 , be functions defined on
, be functions defined on 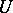 with values in
with values in 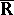 that are continuous in the weak topology of
that are continuous in the weak topology of 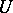 ; let
; let 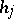 ,
, 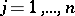 , be functions defined on
, be functions defined on 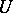 , with values in
, with values in 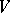 , that are continuous in the weak topologies of the spaces
, that are continuous in the weak topologies of the spaces 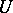 and
and 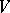 (cf. Weak topology); and let the set
(cf. Weak topology); and let the set  be non-empty. Consider the problem of finding those
be non-empty. Consider the problem of finding those  for which
for which
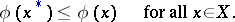 | (*) |
For the function
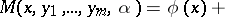 |
 |
with  ,
, 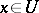 ,
, 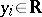 ,
, 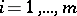 , consider the problem of finding those
, consider the problem of finding those 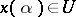 and
and 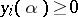 ,
, 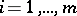 , for which
, for which
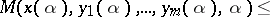 |
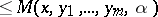 |
for all 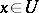 ,
, 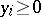 ,
, 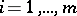 . If
. If
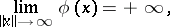 |
then any weak limit point of an arbitrary sequence 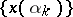 ,
, 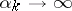 ,
, 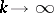 , is a solution of the problem (*) and, moreover,
, is a solution of the problem (*) and, moreover,
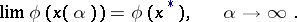 |
References
| [1] | N.N. Moiseev, Yu.P. Ivanilov, E.M. Stolyarova, "Methods of optimization" , Moscow (1978) (In Russian) |
| [2] | F.P. Vasil'ev, "Numerical methods for the solution of extremum problems" , Moscow (1980) (In Russian) |
| [3] | A.V. Fiacco, G.P. MacCormick, "Nonlinear programming: Sequential unconstrained minimization techniques" , Wiley (1968) |
| [4] | J. Cea, "Lectures on optimization: theory and algorithms" , Springer (1978) |
Comments
In the last two decades, new developments in the area of penalty function methods, namely multiplier penalty function methods (or augmented Lagrangian methods) and exact penalty function methods, have replaced for the most part the use of pure penalty function methods. See [a1].
References
| [a1] | R. Fletcher, "Practical methods of optimization" , Wiley (1987) |
| [a2] | D.C. Luenberger, "Optimization by vector space methods" , Wiley (1969) |
| [a3] | A.L. Peressini, F.E. Sullivan, J.J. Uhl, "The mathematics of nonlinear programming" , Springer (1988) |
Penalty functions, method of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Penalty_functions,_method_of&oldid=13425