Pell equation
A Diophantine equation (cf. Diophantine equations) of the form
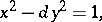 | (1) |
as well as the more general equation
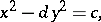 | (2) |
where  is a positive integer,
is a positive integer,  is an irrational number,
is an irrational number,  is an integer, and the unknowns
is an integer, and the unknowns  and
and  are integers.
are integers.
If  ,
,  are the convergent fractions for the expansion of
are the convergent fractions for the expansion of 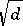 in a continued fraction with period
in a continued fraction with period 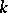 , then the positive solutions to (1) take the form
, then the positive solutions to (1) take the form
 |
where  is any natural number such that
is any natural number such that 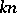 is even.
is even.
All the solutions to (1) are derived from the formula
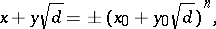 |
where  is any integer and
is any integer and 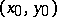 is the solution with the least positive values for the unknowns. The general equation (2) either has no solutions at all or has infinitely many. For
is the solution with the least positive values for the unknowns. The general equation (2) either has no solutions at all or has infinitely many. For 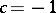 , solutions exist if and only if
, solutions exist if and only if  is odd. For
is odd. For  , (2) always has solutions. The solutions to the Pell equation for
, (2) always has solutions. The solutions to the Pell equation for  are used in determining the units of the quadratic field
are used in determining the units of the quadratic field 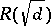 . The solutions to a Pell equation are used to determine automorphisms of a binary quadratic form
. The solutions to a Pell equation are used to determine automorphisms of a binary quadratic form 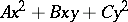 ; these enable one to use one solution to the Diophantine equation
; these enable one to use one solution to the Diophantine equation 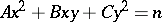 to obtain an infinite set of solutions.
to obtain an infinite set of solutions.
Equation (1) was examined by W. Brouncker (1657), P. Fermat and J. Wallis. L. Euler, on account of a misunderstanding, ascribed it to J. Pell.
References
| [1] | A.Z. Walfisz, "Pell's equation" , Tbilisi (1952) (In Russian) |
| [2] | A.D. Gel'fond, "The solution of equations in integers" , Noordhoff (1960) (Translated from Russian) |
| [3] | W.J. Leveque, "Topics in number theory" , 1 , Addison-Wesley (1965) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1979) |
Pell equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pell_equation&oldid=11604