Difference between revisions of "Path-connected space"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48143 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A [[Topological space|topological space]] in which any two points can be joined by a continuous image of a simple arc; that is, a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718201.png" /> for any two points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718202.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718203.png" /> of which there is a [[Continuous mapping|continuous mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718204.png" /> of the unit interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718205.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718206.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718207.png" />. A path-connected Hausdorff space is a Hausdorff space in which any two points can be joined by a simple arc, or (what amounts to the same thing) a Hausdorff space into which any mapping of a zero-dimensional sphere is homotopic to a constant mapping. Every path-connected space is connected (cf. [[Connected space|Connected space]]). A continuous image of a path-connected space is path-connected. |
| − | p0718201.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | -- | ||
| − | + | Path-connected spaces play an important role in homotopic topology. If a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718208.png" /> is path-connected and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p0718209.png" />, then the homotopy groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182011.png" /> are isomorphic, and this isomorphism is uniquely determined up to the action of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182012.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182013.png" /> is a fibration with path-connected base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182014.png" />, then any two fibres have the same [[Homotopy type|homotopy type]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182015.png" /> is a weak fibration (a [[Serre fibration|Serre fibration]]) over a path-connected base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182016.png" />, then any two fibres have the same weak homotopy type. | |
| − | |||
| − | + | The multi-dimensional generalization of path connectedness is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182018.png" />-connectedness (connectedness in dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182019.png" />). A space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182020.png" /> is said to be connected in dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182022.png" /> if any mapping of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182023.png" />-dimensional sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182024.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182025.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182026.png" />, is homotopic to a constant mapping. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ====References==== | |
| − | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966)</TD></TR></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | A connected space is not necessarily path-connected. It is not true that in an arbitrary path-connected space any two points can be joined by a simple arc: consider the two-point [[Sierpinski space]] | + | A connected space is not necessarily path-connected. It is not true that in an arbitrary path-connected space any two points can be joined by a simple arc: consider the two-point [[Sierpinski space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182027.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182028.png" /> is open and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182029.png" /> is not. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182030.png" /> defined by |
| − | in which | ||
| − | is open and | ||
| − | is not. The mapping | ||
| − | defined by | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182031.png" /></td> </tr></table> | |
| − | |||
is continuous and connects 0 and 1. A space in which any two points can be joined by a simple arc is called arcwise connected. Thus, path-connected Hausdorff spaces are arcwise connected. | is continuous and connects 0 and 1. A space in which any two points can be joined by a simple arc is called arcwise connected. Thus, path-connected Hausdorff spaces are arcwise connected. | ||
Revision as of 14:52, 7 June 2020
A topological space in which any two points can be joined by a continuous image of a simple arc; that is, a space 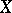 for any two points
for any two points 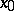 and
and 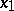 of which there is a continuous mapping
of which there is a continuous mapping 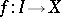 of the unit interval
of the unit interval 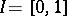 such that
such that 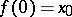 and
and 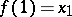 . A path-connected Hausdorff space is a Hausdorff space in which any two points can be joined by a simple arc, or (what amounts to the same thing) a Hausdorff space into which any mapping of a zero-dimensional sphere is homotopic to a constant mapping. Every path-connected space is connected (cf. Connected space). A continuous image of a path-connected space is path-connected.
. A path-connected Hausdorff space is a Hausdorff space in which any two points can be joined by a simple arc, or (what amounts to the same thing) a Hausdorff space into which any mapping of a zero-dimensional sphere is homotopic to a constant mapping. Every path-connected space is connected (cf. Connected space). A continuous image of a path-connected space is path-connected.
Path-connected spaces play an important role in homotopic topology. If a space 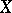 is path-connected and
is path-connected and  , then the homotopy groups
, then the homotopy groups 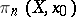 and
and  are isomorphic, and this isomorphism is uniquely determined up to the action of the group
are isomorphic, and this isomorphism is uniquely determined up to the action of the group 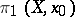 . If
. If 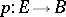 is a fibration with path-connected base
is a fibration with path-connected base 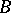 , then any two fibres have the same homotopy type. If
, then any two fibres have the same homotopy type. If  is a weak fibration (a Serre fibration) over a path-connected base
is a weak fibration (a Serre fibration) over a path-connected base 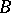 , then any two fibres have the same weak homotopy type.
, then any two fibres have the same weak homotopy type.
The multi-dimensional generalization of path connectedness is 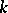 -connectedness (connectedness in dimension
-connectedness (connectedness in dimension 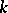 ). A space
). A space 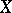 is said to be connected in dimension
is said to be connected in dimension  if any mapping of an
if any mapping of an  -dimensional sphere
-dimensional sphere  into
into 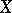 , where
, where 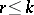 , is homotopic to a constant mapping.
, is homotopic to a constant mapping.
References
| [1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
Comments
A connected space is not necessarily path-connected. It is not true that in an arbitrary path-connected space any two points can be joined by a simple arc: consider the two-point Sierpinski space 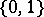 in which
in which 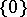 is open and
is open and  is not. The mapping
is not. The mapping 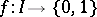 defined by
defined by
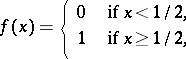 |
is continuous and connects 0 and 1. A space in which any two points can be joined by a simple arc is called arcwise connected. Thus, path-connected Hausdorff spaces are arcwise connected.
References
| [a1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [a2] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. 15ff, 130 |
Path-connected space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Path-connected_space&oldid=48143