Pasch configuration
quadrilateral
A collection of four triples isomorphic to  ,
, 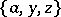 ,
,  ,
, 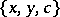 . Pasch configurations have been studied extensively in the context of Steiner triple systems.
. Pasch configurations have been studied extensively in the context of Steiner triple systems.
A Steiner triple system of order  ,
, 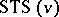 , is an ordered pair
, is an ordered pair 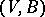 where
where 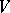 is a set of cardinality
is a set of cardinality  , called elements or points, and
, called elements or points, and 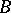 is a collection of triples, also called lines or blocks, which collectively have the property that every pair of distinct elements of
is a collection of triples, also called lines or blocks, which collectively have the property that every pair of distinct elements of 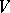 occur in precisely one triple.
occur in precisely one triple. 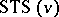 exist if and only if
exist if and only if  or
or 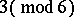 , [a5] (cf. also Steiner system). To within isomorphism, the Steiner triple systems of orders
, [a5] (cf. also Steiner system). To within isomorphism, the Steiner triple systems of orders 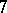 and
and  are unique, but for all greater orders the structure is not unique. A
are unique, but for all greater orders the structure is not unique. A 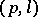 -configuration in a Steiner triple system is a collection of
-configuration in a Steiner triple system is a collection of 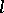 lines whose union contains precisely
lines whose union contains precisely 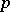 points. A configuration whose number of occurrences in an
points. A configuration whose number of occurrences in an 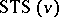 depends only upon the order
depends only upon the order  and not on the structure of the
and not on the structure of the 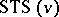 is called constant and otherwise variable. There are two configurations with
is called constant and otherwise variable. There are two configurations with 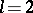 and five with
and five with 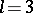 , all of which are constant. There are
, all of which are constant. There are 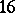 configurations with
configurations with 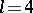 , of which the Pasch configuration or quadrilateral is the unique
, of which the Pasch configuration or quadrilateral is the unique 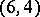 -configuration and the one containing the least number of points. Five of the
-configuration and the one containing the least number of points. Five of the 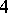 -line configurations are constant but the Pasch configuration is variable. It was shown in [a7] that the number of occurrences of all the other variable
-line configurations are constant but the Pasch configuration is variable. It was shown in [a7] that the number of occurrences of all the other variable 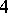 -line configurations can be expressed in terms of the order
-line configurations can be expressed in terms of the order  and the number
and the number  of Pasch configurations in the
of Pasch configurations in the 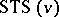 .
.
The above gives motivation to the problem of constructing 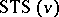 containing no Pasch configurations, so-called anti-Pasch or quadrilateral free Steiner triple systems. A solution for
containing no Pasch configurations, so-called anti-Pasch or quadrilateral free Steiner triple systems. A solution for 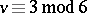 was first given by A.E. Brouwer ([a1], see also [a8]) and it was a long-standing conjecture that anti-Pasch
was first given by A.E. Brouwer ([a1], see also [a8]) and it was a long-standing conjecture that anti-Pasch  also exist for all
also exist for all 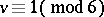 ,
, 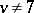 or
or 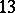 . This was settled in the affirmative in two papers, [a6] and [a10], published in 2000. The proof resolves the first case of a conjecture by P. Erdős, [a3], that for every
. This was settled in the affirmative in two papers, [a6] and [a10], published in 2000. The proof resolves the first case of a conjecture by P. Erdős, [a3], that for every 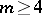 there is an integer
there is an integer  so that for every
so that for every 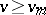 ,
, 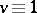 or
or 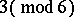 , there is an
, there is an 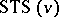 avoiding
avoiding 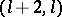 -configurations for
-configurations for 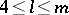 . Anti-Pasch
. Anti-Pasch 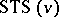 have application to erasure-correcting codes, [a2]. The theoretical maximum number of Pasch configurations in an
have application to erasure-correcting codes, [a2]. The theoretical maximum number of Pasch configurations in an 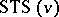 is
is 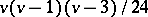 but this is achieved only in the point-line designs obtained from the projective spaces
but this is achieved only in the point-line designs obtained from the projective spaces 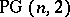 , [a9].
, [a9].
The Pasch configuration is an example of a so-called trade. A pair of distinct collections of blocks 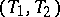 is said to be mutually
is said to be mutually 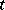 -balanced if each
-balanced if each 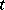 -element subset of the base set
-element subset of the base set  is contained in precisely the same number of blocks of
is contained in precisely the same number of blocks of  as of
as of 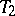 . Each collection
. Each collection 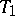 ,
, 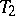 is then referred to as a trade. The Pasch configuration is the smallest trade that can occur in a Steiner triple system. If
is then referred to as a trade. The Pasch configuration is the smallest trade that can occur in a Steiner triple system. If 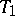 is the collection
is the collection 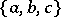 ,
, 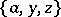 ,
, 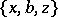 ,
, 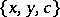 , then, by replacing each triple with its complement, a collection
, then, by replacing each triple with its complement, a collection 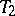 ,
, 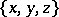 ,
, 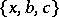 ,
, 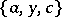 ,
, 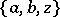 , is obtained which contains precisely the same pairs as
, is obtained which contains precisely the same pairs as  . This transformation is known as a Pasch switch, and when applied to a Steiner triple system yields another, usually non-isomorphic, Steiner triple system. There are
. This transformation is known as a Pasch switch, and when applied to a Steiner triple system yields another, usually non-isomorphic, Steiner triple system. There are 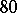 non-isomorphic
non-isomorphic 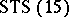 s, of which precisely one is anti-Pasch. It was shown in [a4] that all of the remaining
s, of which precisely one is anti-Pasch. It was shown in [a4] that all of the remaining  systems can be obtained from one another by successive Pasch switches. Other relevant papers in this area are [a11] and [a12].
systems can be obtained from one another by successive Pasch switches. Other relevant papers in this area are [a11] and [a12].
The number of Pasch configurations and their distribution within a Steiner triple system is an invariant and provides a simple and useful test to help in determining whether two systems are isomorphic.
References
| [a1] | A.E. Brouwer, "Steiner triple systems without forbidden subconfigurations" Rept. Math. Centrum Amsterdam , ZW104/77 (1977) |
| [a2] | C.J. Colbourn, J.H. Dinitz, D.R. Stinson, "Applications of combinatorial designs to communications, cryptography and networking" London Math. Soc. Lecture Notes , 267 (1999) pp. 37–100 |
| [a3] | P. Erdös, "Problems and results in combinatorial analysis" Creation in Math. , 9 (1976) pp. 25 |
| [a4] | P.B. Gibbons, "Computing techniques for the construction and analysis of block designs" Techn. Rept. Dept. Computer Sci. Univ. Toronto , 92 (1976) |
| [a5] | T.P. Kirkman, "On a problem in combinations" Cambridge and Dublin Math. J. , 2 (1847) pp. 191–204 |
| [a6] | A.C.H. Ling, C.J. Colbourn, M.J. Grannell, T.S. Griggs, "Construction techniques for anti-Pasch Steiner triple systems" J. London Math. Soc. (2) , 61 (2000) pp. 641–657 |
| [a7] | M.J. Grannell, T.S. Griggs, E. Mendelsohn, "A small basis for four-line configurations in Steiner triple systems" J. Combin. Designs , 3 (1995) pp. 51–59 |
| [a8] | T.S. Griggs, J.P. Murphy, J.S. Phelan, "Anti-Pasch Steiner triple systems" J. Combin. Inform. & Syst. Sci. , 15 (1990) pp. 79–84 |
| [a9] | D.R. Stinson, Y.J. Wei, "Some results on quadrilaterals in Steiner triple systems" Discr. Math. , 105 (1992) pp. 207–219 |
| [a10] | M.J. Grannell, T.S. Griggs, C.A. Whitehead, "The resolution of the anti-Pasch conjecture" J. Combin. Designs , 8 (2000) pp. 300–309 |
| [a11] | M.J. Grannell, T.S. Griggs, J.P. Murphy, "Twin Steiner triple systems" Discr. Math. , 167/8 (1997) pp. 341–352 |
| [a12] | M.J. Grannell, T.S. Griggs, J.P. Murphy, "Switching cycles in Steiner triple systems" Utilitas Math. , 56 (1999) pp. 3–21 |
Pasch configuration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pasch_configuration&oldid=14037