Parallel straight lines
in Euclidean geometry
Lines that lie in one plane and that do not intersect. In absolute geometry there passes through a point not lying on a given line at least one line that does not intersect the given one. In Euclidean geometry there is only one such line. This fact is equivalent to Euclid's fifth postulate (on parallels). In Lobachevskii geometry in the plane there pass through a point 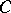 (see Fig.) outside a given line
(see Fig.) outside a given line 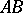 infinitely-many lines that do not intersect
infinitely-many lines that do not intersect  . Of these only two are called parallel to
. Of these only two are called parallel to 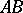 . A line
. A line 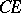 is said to be parallel to
is said to be parallel to 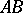 in the direction from
in the direction from 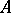 to
to 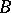 if: 1)
if: 1) 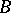 and
and 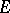 lie on the same side of
lie on the same side of 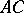 ; 2)
; 2) 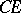 does not intersect
does not intersect 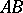 ; and 3) every ray within the angle
; and 3) every ray within the angle 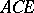 intersects the line
intersects the line 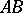 . The line
. The line 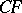 parallel to
parallel to 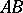 in the direction from
in the direction from 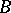 to
to 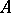 is defined similarly.
is defined similarly.
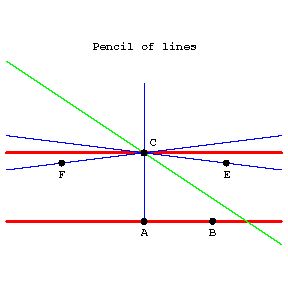
Figure: p071380a
Comments
References
| [a1] | H.S.M. Coxeter, "Parallel lines" Canad. Math. Bulletin , 21 : 4 (1978) pp. 385–397 |
| [a2] | M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974) |
| [a3] | D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968) |
Parallel straight lines. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parallel_straight_lines&oldid=12124