Pap adjoint theorem

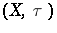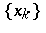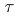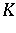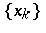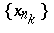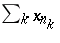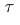If is a topological vector space, a sequence in X is said to be a - sequence if every subsequence of has a further subsequence such that the subseries is -convergent to an element of .

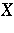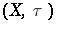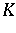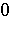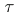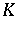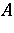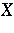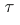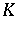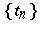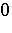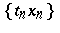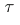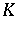A topological vector space is said to be a -space if every sequence which converges to is a - sequence. A subset of is said to be - bounded if for every sequence and every scalar sequence converging to , the sequence is a - sequence.

Let 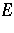and 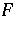be Hausdorff locally convex topological vector spaces (cf. also Locally convex space; Hausdorff space) and let 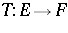be a linear mapping. The domain of the adjoint operator, 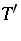, is defined to be

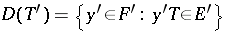and 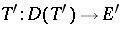is defined by .

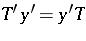The first adjoint theorem was proved by E. Pap [a3] for operators defined on pre-Hilbert 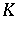-spaces. There exists a pre-Hilbert 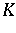-space which is not a Hilbert space, [a2]. A generalization of the adjoint theorem for normed spaces was given in [a1], [a4]. It reads as follows.

Let 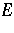be a normed 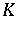-space, let 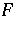be a normed space and let 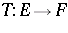be a linear operator. Then the adjoint operator 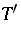is a bounded linear operator on .

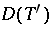In the proofs of all these theorems, so-called diagonal theorems were used (cf. also Diagonal theorem). As a simple consequence, a proof of the closed-graph theorem without the Baire category argumentation was obtained, [a3], [a4], [a6], [a8], [a9].

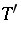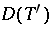There is a locally convex generalization of the adjoint theorem [a5], [a7]: is sequentially continuous with respect to the relative - (weak) topology on and the topology on 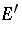of uniform convergence on 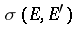--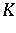convergent sequences. In particular, 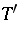is bounded with respect to these topologies.

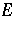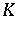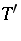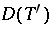A special case is obtained when is a normed -space. Then maps weak- bounded subsets of to norm-bounded subsets of 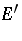. In particular, 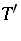is norm-bounded.

References

[a1]	P. Antosik, Swartz, C., "Matrix methods in analysis" , Lecture Notes Math. , 1113 , Springer (1985)
[a2]	C. Kliś, "An example of non-complete normed (K)-space" Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys. , 26 (1976) pp. 415–420
[a3]	E. Pap, "Functional analysis with K-convergence" , Proc. Conf. Convergence, Bechyne, Czech. , Akad. Berlin (1984) pp. 245–250
[a4]	E. Pap, "The adjoint operator and K-convergence" Univ. u Novom Sadu Zb. Rad. Prirod.-Mat. Fak. Ser. Mat. , 15 : 2 (1985) pp. 51–56
[a5]	E. Pap, "Null-additive set functions" , Kluwer Acad. Publ. &Ister Sci. (1995)
[a6]	E. Pap, C. Swartz, "The closed graph theorem for locally convex spaces" Boll. Un. Mat. Ital. , 7 : 4-B (1990) pp. 109–111
[a7]	E. Pap, C. Swartz, "A locally convex version of adjoint theorem" Univ. u Novom Sadu Zb. Rad. Prirod. - Mat. Fak. Ser. Mat. , 24 : 2 (1994) pp. 63–68
[a8]	C. Swartz, "The closed graph theorem without category" Bull. Austral. Math. Soc. , 36 (1987) pp. 283–288
[a9]	C. Swartz, "Introduction to functional analysis" , M. Dekker (1992)