Over-convergence
Convergence of a certain subsequence of partial sums of a series in a domain that is larger than the domain of convergence of the series. The following theorems on over-convergence hold:
1) If for a power series
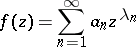 |
with radius of convergence  ,
, 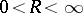 , the exponents
, the exponents  are such that for an infinite set of values
are such that for an infinite set of values  of
of  :
:
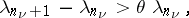 |
where  is a fixed positive number, then the sequence of partial sums of orders
is a fixed positive number, then the sequence of partial sums of orders  ,
,
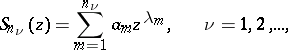 |
converges uniformly in a sufficiently small neighbourhood of each point 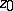 of the circle
of the circle  on which the sum of the series for
on which the sum of the series for  is regular.
is regular.
2) If
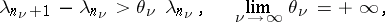 |
then the sequence  converges uniformly in any closed bounded part of the domain of existence of
converges uniformly in any closed bounded part of the domain of existence of 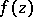 .
.
The following theorem also holds (the converse of 1)): If a power series
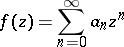 |
with radius of convergence 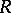 ,
,  , has a subsequence of partial sums that is uniformly convergent in some neighbourhood of
, has a subsequence of partial sums that is uniformly convergent in some neighbourhood of 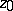 ,
, 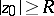 , then this power series can be represented as the sum of a series with radius of convergence greater than
, then this power series can be represented as the sum of a series with radius of convergence greater than 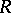 and a lacunary power series:
and a lacunary power series:
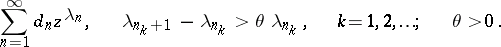 |
The first theorem is true for many other series, in particular for Dirichlet series.
References
| [1] | L. Bieberbach, "Analytische Fortsetzung" , Springer (1955) pp. Sect. 3 |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [3] | A.F. Leont'ev, "Exponential series" , Moscow (1976) (In Russian) |
Comments
References
| [a1] | L. [L. Il'ev] Ilieff, "Analytische Nichtfortsetzbarkeit und Überkonvergenz einiger Klassen von Potenzreihen" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
Over-convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Over-convergence&oldid=18212