Osculating circle
From Encyclopedia of Mathematics
at a given point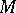 
of a curve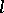 
The circle that has contact of order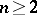 
with 
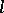at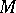 
(see Osculation). If the curvature of 
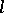at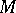 
is zero, then the osculating circle degenerates into a straight line. The radius of the osculating circle is called the radius of curvature of 
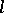at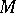 
, and its centre the centre of curvature (see Fig.). If 
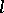is the plane curve given by an equation 
, then the radius of the osculating circle is given by
 |
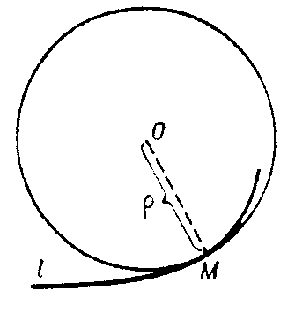
Figure: o070540a
If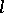 
is the spatial curve given by equations
 |
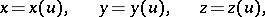then the radius of the osculating circle is given by
 |
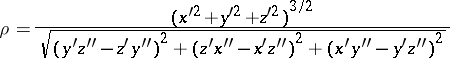(where the primes denote differentiation with respect to 
).
Comments
References
| [a1] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 39 |
| [a2] | D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 14 |
How to Cite This Entry:
Osculating circle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_circle&oldid=14753
Osculating circle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_circle&oldid=14753
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article