Orientation
A formalization and far-reaching generalization of the concept of direction on a curve. The orientation of special classes of spaces is defined (cf. Manifold; Vector bundle; Poincaré complex, etc.). The modern view of orientation is given in Generalized cohomology theories.
In classical mathematics, an orientation is the choice of an equivalence class of coordinate systems, where two coordinate systems belong to the same class if they are positively related (in a specific sense).
In the case of a finite-dimensional vector space 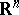 , a coordinate system is given by a basis, and two bases are positively related if the determinant of the transition matrix from one to the other is positive. There are two classes here. In a complex space
, a coordinate system is given by a basis, and two bases are positively related if the determinant of the transition matrix from one to the other is positive. There are two classes here. In a complex space 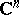 with complex basis
with complex basis  , a real basis is given by
, a real basis is given by 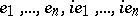 , considering the space as
, considering the space as 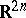 . Any two real bases arising in this way from complex bases are positively related (i.e. a complex structure defines an orientation on
. Any two real bases arising in this way from complex bases are positively related (i.e. a complex structure defines an orientation on  ).
).
In a line, plane or, generally, a real affine space 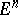 , a coordinate system is given by the choice of a point (origin) and a basis. The change of coordinates is defined by a translation (changing the origin) and a change of basis. This change is positive if the matrix of the base change has positive determinant. (For example, an even permutation of the vectors in the basis.) Two coordinate systems define the same orientation if one of them can be continuously transformed into the other, i.e. if a family of coordinate systems
, a coordinate system is given by the choice of a point (origin) and a basis. The change of coordinates is defined by a translation (changing the origin) and a change of basis. This change is positive if the matrix of the base change has positive determinant. (For example, an even permutation of the vectors in the basis.) Two coordinate systems define the same orientation if one of them can be continuously transformed into the other, i.e. if a family of coordinate systems 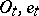 connecting the given systems
connecting the given systems 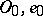 and
and 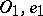 and depending continuously on
and depending continuously on 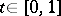 exists. Reflection in an
exists. Reflection in an 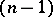 -dimensional plane gives the opposite orientation, i.e. the other class.
-dimensional plane gives the opposite orientation, i.e. the other class.
Classes of coordinate systems can be defined by different geometric figures. If a figure 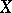 is related by a specific rule to a coordinate system, then its mirror image should be related by the same rule to a coordinate system with the opposite orientation. In this way,
is related by a specific rule to a coordinate system, then its mirror image should be related by the same rule to a coordinate system with the opposite orientation. In this way, 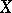 (along with the given rule) defines an orientation. For example, in the plane
(along with the given rule) defines an orientation. For example, in the plane 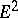 , a circle with a given direction of traversal defines a coordinate system from one class by the rule that the origin is at the centre of the circle, with the first basis vector taken arbitrarily while the second is taken so that the rotation from the first to the second through the smaller angle is the direction of traversal on the circle. In
, a circle with a given direction of traversal defines a coordinate system from one class by the rule that the origin is at the centre of the circle, with the first basis vector taken arbitrarily while the second is taken so that the rotation from the first to the second through the smaller angle is the direction of traversal on the circle. In 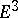 , a frame can be related to a screw. The first vector goes in the direction the screw moves when being screwed in, and the rotation from the second vector to the third coincides with the rotation of the screw as it is screwed in (it is supposed that all screws are threaded in the same way). A basis (frame) can also be defined in a well-known way by using the thumb and first two fingers on one's hand, as in the right-hand rule.
, a frame can be related to a screw. The first vector goes in the direction the screw moves when being screwed in, and the rotation from the second vector to the third coincides with the rotation of the screw as it is screwed in (it is supposed that all screws are threaded in the same way). A basis (frame) can also be defined in a well-known way by using the thumb and first two fingers on one's hand, as in the right-hand rule.
If an orientation of 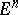 is given, then every half-space
is given, then every half-space 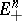 defines an orientation on the boundary plane
defines an orientation on the boundary plane 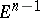 . For example, it may be agreed that if the last
. For example, it may be agreed that if the last 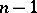 vectors in an oriented basis lie in
vectors in an oriented basis lie in 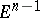 , while the first vector points outwards from
, while the first vector points outwards from 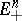 , then the last
, then the last 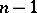 vectors define the orientation of
vectors define the orientation of 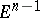 . In
. In 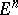 an orientation can be defined by the order of the vertices of an
an orientation can be defined by the order of the vertices of an  -dimensional simplex (a triangle in
-dimensional simplex (a triangle in 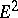 , a tetrahedron in
, a tetrahedron in 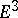 ). A basis is defined by choosing the origin at the first vertex, while the vectors of the basis point to the other vertices. Two orders define the same orientation if and only if they differ by an even permutation. A simplex with a fixed order of vertices up to an even permutation is said to be oriented. Every
). A basis is defined by choosing the origin at the first vertex, while the vectors of the basis point to the other vertices. Two orders define the same orientation if and only if they differ by an even permutation. A simplex with a fixed order of vertices up to an even permutation is said to be oriented. Every 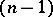 -face
-face 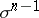 of an oriented simplex has an induced orientation: If the first vertex does not belong to
of an oriented simplex has an induced orientation: If the first vertex does not belong to 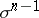 , then the order of the others is taken to be positive for
, then the order of the others is taken to be positive for 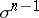 .
.
In a connected manifold 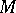 , the coordinate system takes the form of an atlas: A set of charts (cf. Chart) which cover
, the coordinate system takes the form of an atlas: A set of charts (cf. Chart) which cover 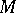 . The atlas is said to be orienting if the coordinate transformations between charts are all positive. In the case of a differentiable manifold this means that the Jacobians of the coordinate transformations between any two charts are positive at every point. If an orienting atlas exists, then
. The atlas is said to be orienting if the coordinate transformations between charts are all positive. In the case of a differentiable manifold this means that the Jacobians of the coordinate transformations between any two charts are positive at every point. If an orienting atlas exists, then 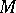 is orientable. In this case, all orienting atlases divide into two classes such that the transition from the charts of one atlas to the charts of another is positive if and only if both atlases belong to the same class. A choice of this class is called an orientation of the manifold. This choice can be made by choosing one chart or local orientation at a point
is orientable. In this case, all orienting atlases divide into two classes such that the transition from the charts of one atlas to the charts of another is positive if and only if both atlases belong to the same class. A choice of this class is called an orientation of the manifold. This choice can be made by choosing one chart or local orientation at a point 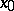 (connected charts which contain
(connected charts which contain 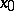 naturally divide into two classes). In the case of a differentiable manifold, a local orientation can be defined by choosing a basis in the tangent plane at the point
naturally divide into two classes). In the case of a differentiable manifold, a local orientation can be defined by choosing a basis in the tangent plane at the point 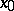 (for example, a rotation direction on the circle can be defined by choosing one tangent vector). If
(for example, a rotation direction on the circle can be defined by choosing one tangent vector). If 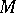 has a boundary and is oriented, then the boundary is also orientable, for example according to the rule: At a point of the boundary, a basis is taken which orients
has a boundary and is oriented, then the boundary is also orientable, for example according to the rule: At a point of the boundary, a basis is taken which orients 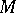 , the first vector of which is directed from
, the first vector of which is directed from 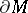 , while the other vectors lie in the tangent plane to the boundary; these latter vectors are taken to be an orienting basis of the boundary.
, while the other vectors lie in the tangent plane to the boundary; these latter vectors are taken to be an orienting basis of the boundary.
Along any path 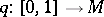 , a chain of charts can be chosen such that two neighbouring charts are positively connected. Thus, an orientation at the point
, a chain of charts can be chosen such that two neighbouring charts are positively connected. Thus, an orientation at the point 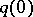 defines an orientation at the point
defines an orientation at the point 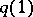 , and this relation depends on the path
, and this relation depends on the path 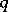 only up to its continuous deformation when its ends are fixed. If
only up to its continuous deformation when its ends are fixed. If 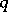 is a loop, i.e.
is a loop, i.e. 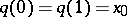 , then
, then 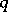 is called an orientation-reserving loop if these orientations are opposite. A homomorphism of the fundamental group
is called an orientation-reserving loop if these orientations are opposite. A homomorphism of the fundamental group 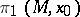 into a group of order 2 arises: The orientation-reversing loops are sent to
into a group of order 2 arises: The orientation-reversing loops are sent to 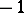 , while the others are sent to
, while the others are sent to 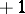 . Through this homomorphism a covering is created, which is a two-sheeted covering in the case of a non-orientable manifold. It is said to be orienting (since the covering space will be orientable). This same homomorphism defines a line bundle over
. Through this homomorphism a covering is created, which is a two-sheeted covering in the case of a non-orientable manifold. It is said to be orienting (since the covering space will be orientable). This same homomorphism defines a line bundle over 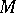 which is trivial if and only if
which is trivial if and only if 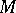 is orientable. For a differentiable
is orientable. For a differentiable 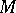 it can be defined as the bundle
it can be defined as the bundle 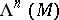 of differential forms of order
of differential forms of order  . It has a non-zero section only in the orientable case and then such a section simultaneously defines a volume form on
. It has a non-zero section only in the orientable case and then such a section simultaneously defines a volume form on 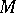 and an orientation. This bundle has a classifying mapping
and an orientation. This bundle has a classifying mapping 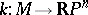 . The manifold
. The manifold 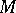 is orientable if and only if the class
is orientable if and only if the class 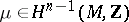 which is the image of the class dual to
which is the image of the class dual to 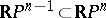 , is not equal to zero. It is dual to a cycle whose support is the manifold which is the pre-image of
, is not equal to zero. It is dual to a cycle whose support is the manifold which is the pre-image of 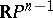 under the mapping
under the mapping 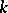 , taken in general position. This cycle is said to be orienting, since its complement is orientable: If
, taken in general position. This cycle is said to be orienting, since its complement is orientable: If 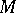 is cut by means of the cycle, then an orientable manifold is obtained.
is cut by means of the cycle, then an orientable manifold is obtained. 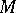 is itself orientable (non-orientable) if and only if a disconnected manifold (a connected complement) is obtained after the cut. For example, in
is itself orientable (non-orientable) if and only if a disconnected manifold (a connected complement) is obtained after the cut. For example, in 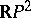 , a projective line
, a projective line 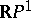 serves as orienting cycle.
serves as orienting cycle.
A triangulated manifold 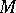 (or a pseudo-manifold) is orientable if it is possible to orient all
(or a pseudo-manifold) is orientable if it is possible to orient all  -dimensional simplices such that two simplices with a common
-dimensional simplices such that two simplices with a common  -dimensional face induce opposite orientations on the face. A closed chain of
-dimensional face induce opposite orientations on the face. A closed chain of  -dimensional simplices each two neighbours of which have a common
-dimensional simplices each two neighbours of which have a common 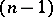 -face is said to be orientation-reversing if these simplices can be oriented such that the first and last simplices induce coinciding orientations on the common face, while the other neighbours induce opposite orientations.
-face is said to be orientation-reversing if these simplices can be oriented such that the first and last simplices induce coinciding orientations on the common face, while the other neighbours induce opposite orientations.
An orientation can be defined in the language of homology theory thus: For a connected orientable manifold without boundary, the homology group 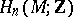 (with closed supports) is isomorphic to
(with closed supports) is isomorphic to 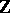 , and the choice of one of the two generators defines an orientation. This is also true for a connected manifold with boundary, using
, and the choice of one of the two generators defines an orientation. This is also true for a connected manifold with boundary, using 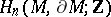 . In the first instance, orientability is a homotopy invariant of
. In the first instance, orientability is a homotopy invariant of 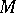 , while in the second, of the pair
, while in the second, of the pair 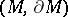 . So, the Möbius strip and the annulus have one and the same homotopy type but a different one if one considers the boundary. A local orientation of the manifold can also be defined by the choice of generators in the group
. So, the Möbius strip and the annulus have one and the same homotopy type but a different one if one considers the boundary. A local orientation of the manifold can also be defined by the choice of generators in the group 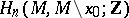 , isomorphic to
, isomorphic to 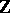 . The homological interpretation of orientation enables this concept to be applied to generalized homology manifolds (cf. Homology manifold).
. The homological interpretation of orientation enables this concept to be applied to generalized homology manifolds (cf. Homology manifold).
Let a fibration 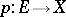 with standard fibre
with standard fibre 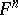 be defined uniquely over a space
be defined uniquely over a space 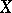 . If the orientation of all fibres can be chosen such that any (non-singular) mapping
. If the orientation of all fibres can be chosen such that any (non-singular) mapping 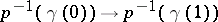 , defined by the path
, defined by the path 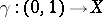 up to a non-singular homotopy, preserves the orientation, then the fibration is oriented, while the choice of the orientation of the fibres is the orientation of the fibration. For example, a Möbius strip, looked at as a vector bundle over a circle, does not possess an orientation, whereas the lateral surface of a cylinder does.
up to a non-singular homotopy, preserves the orientation, then the fibration is oriented, while the choice of the orientation of the fibres is the orientation of the fibration. For example, a Möbius strip, looked at as a vector bundle over a circle, does not possess an orientation, whereas the lateral surface of a cylinder does.
The concept of orientation also allows a natural generalization for the case of an infinite-dimensional manifold modelled on an infinite-dimensional Banach or topological vector space. This requires restrictions on the linear operators which are differentials of transitions from one chart to another: They must not simply belong to the general linear group of all isomorphisms of the structure space, which is homotopically trivial (in the uniform topology) for the majority of classical vector spaces, but must also be contained in a disconnected subgroup of the general linear group. The connected component of the given subgroup will then also provide the "sign" of the orientation. The subgroup usually chosen is the Fredholm group, consisting of those isomorphisms of the structure space for which the difference from the identity isomorphism is a completely-continuous operator.
Orientation in generalized cohomology theories.
Let 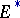 be a multiplicative generalized cohomology theory (hereafter, simply a theory). There is a unit
be a multiplicative generalized cohomology theory (hereafter, simply a theory). There is a unit  for which, given the suspension isomorphism
for which, given the suspension isomorphism  , there is a corresponding element
, there is a corresponding element 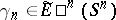 , where
, where  is the
is the  -dimensional sphere.
-dimensional sphere.
Let 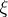 be an
be an  -dimensional vector bundle over an arcwise-connected space
-dimensional vector bundle over an arcwise-connected space 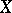 and let
and let 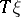 be the Thom space of
be the Thom space of 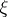 . Let
. Let 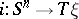 be a standard imbedding, i.e. a homeomorphism on the "fibre" over a point
be a standard imbedding, i.e. a homeomorphism on the "fibre" over a point 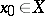 . The element
. The element 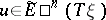 is called an orientation or a Thom class of the bundle
is called an orientation or a Thom class of the bundle 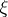 if
if 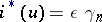 , where
, where  is an invertible element (for example,
is an invertible element (for example, 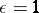 ). A bundle possessing an orientation is orientable in the theory
). A bundle possessing an orientation is orientable in the theory 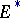 or simply
or simply 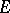 -orientable, while a bundle with a chosen
-orientable, while a bundle with a chosen 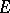 -orientation is
-orientation is 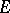 -oriented. The Thom isomorphism
-oriented. The Thom isomorphism 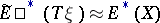 is valid (see [6]). The set of orientations of a given
is valid (see [6]). The set of orientations of a given 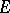 -oriented bundle
-oriented bundle 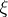 over
over 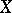 is in one-to-one correspondence with the elements of the group
is in one-to-one correspondence with the elements of the group 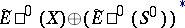 , where
, where 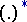 is the group of invertible elements of the ring
is the group of invertible elements of the ring  .
.
The trivial  -dimensional bundle
-dimensional bundle 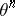 possesses an orientation in any theory
possesses an orientation in any theory 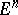 , and if two out of the three bundles
, and if two out of the three bundles 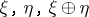 are
are 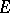 -orientable, then the third is also
-orientable, then the third is also 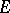 -orientable (see [7]). Moreover, the
-orientable (see [7]). Moreover, the 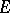 -orientability of
-orientability of 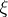 entails the
entails the 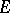 -orientability of
-orientability of  .
.
The concept of 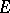 -orientability is also introduced for any bundle in the sense of Hurewicz
-orientability is also introduced for any bundle in the sense of Hurewicz 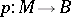 , a fibre of which is homotopically equivalent to a sphere. The cone of the mapping
, a fibre of which is homotopically equivalent to a sphere. The cone of the mapping 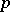 is called the Thom space of this bundle; further definitions are analogous. The definition of orientation of a vector bundle
is called the Thom space of this bundle; further definitions are analogous. The definition of orientation of a vector bundle 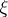 reduces to this if a bundle of unit spheres (in some Riemannian metric on
reduces to this if a bundle of unit spheres (in some Riemannian metric on 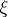 ) associated with
) associated with  is taken as
is taken as 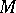 .
. 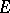 -orientability is an invariant of the stable fibre-wise homotopy type of a vector (sphere) bundle. A bundle which is orientable in one theory is not necessarily orientable in another, but given a ring homomorphism of theories
-orientability is an invariant of the stable fibre-wise homotopy type of a vector (sphere) bundle. A bundle which is orientable in one theory is not necessarily orientable in another, but given a ring homomorphism of theories 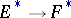 , the property of
, the property of  -orientability follows from
-orientability follows from 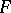 -orientability.
-orientability.
Examples.
1) In the theory 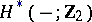 , any vector (sphere) bundle is orientable.
, any vector (sphere) bundle is orientable.
2) In the theory  , those bundles
, those bundles 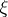 for which the Stiefel–Whitney characteristic class
for which the Stiefel–Whitney characteristic class 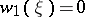 are orientable, i.e. those bundles which are orientable in the classical sense.
are orientable, i.e. those bundles which are orientable in the classical sense.
3) The orientability of a vector bundle 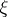 in real
in real 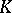 -theory is equivalent to the fact that
-theory is equivalent to the fact that 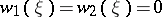 , while in complex
, while in complex 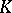 -theory it is equivalent to the fact that
-theory it is equivalent to the fact that 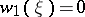 and
and 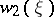 is an integral class [8]. For sphere bundles to be
is an integral class [8]. For sphere bundles to be 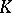 -orientable, this condition is necessary, though not sufficient.
-orientable, this condition is necessary, though not sufficient.
4) In the theory 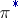 of stable cohomotopy groups, only bundles of trivial stable fibre-wise homotopy type are orientable.
of stable cohomotopy groups, only bundles of trivial stable fibre-wise homotopy type are orientable.
In the problem of describing the class of bundles which are orientable in a given theory, the following general result holds. Let a topological group 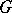 act on
act on 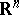 and let
and let 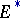 be a certain theory. A space
be a certain theory. A space 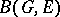 with a universal
with a universal 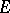 -oriented bundle over it exists (see [7], where an explicit construction is given) which classifies the
-oriented bundle over it exists (see [7], where an explicit construction is given) which classifies the 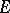 -oriented vector bundles with structure group
-oriented vector bundles with structure group 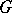 , i.e. for any (arcwise connected) space
, i.e. for any (arcwise connected) space 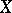 , the set of
, the set of 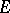 -oriented
-oriented 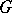 -vector bundles over
-vector bundles over 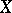 is in natural one-to-one correspondence with a set
is in natural one-to-one correspondence with a set 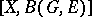 of homotopy classes of mappings
of homotopy classes of mappings 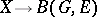 . This is also true for sphere bundles and "good" monoids
. This is also true for sphere bundles and "good" monoids 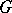 .
.
The opposite problem consists of describing a theory in which a given bundle (or class of bundles) is orientable. It is known that if in a theory 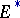 all vector bundles are orientable, then
all vector bundles are orientable, then
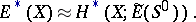 |
Moreover, 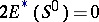 . In this context, the conditions on the theory
. In this context, the conditions on the theory 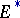 are weakened, for example, the condition of commutativity of multiplication is dropped, etc. For any theory
are weakened, for example, the condition of commutativity of multiplication is dropped, etc. For any theory 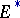 in which all complex bundles are orientable, there is a homomorphism of theories
in which all complex bundles are orientable, there is a homomorphism of theories 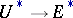 , where
, where 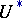 is the theory of unitary cobordism, and this homomorphism is completely defined by the
is the theory of unitary cobordism, and this homomorphism is completely defined by the 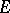 -orientation of the canonical bundles
-orientation of the canonical bundles 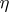 over
over 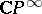 . The same is true for
. The same is true for  -bundles (see Cobordism). Constructing for a given class of vector bundles the universal theory, which maps onto any other theory in which the class of bundles is orientable, has yet to be carried out (1989).
-bundles (see Cobordism). Constructing for a given class of vector bundles the universal theory, which maps onto any other theory in which the class of bundles is orientable, has yet to be carried out (1989).
An element 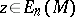 such that the homomorphism
such that the homomorphism 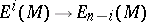 given by
given by 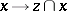 (see [9]) is an isomorphism, is called an orientation (or fundamental class) of the closed
(see [9]) is an isomorphism, is called an orientation (or fundamental class) of the closed  -dimensional manifold
-dimensional manifold 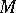 (or, more generally, of the Poincaré complex of formal dimension
(or, more generally, of the Poincaré complex of formal dimension  ) in the theory
) in the theory 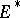 . This isomorphism is the so-called Poincaré duality isomorphism. A manifold (Poincaré complex) is
. This isomorphism is the so-called Poincaré duality isomorphism. A manifold (Poincaré complex) is 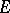 -orientable if and only if its normal bundle is
-orientable if and only if its normal bundle is 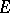 -orientable. An orientation is also defined for manifolds (Poincaré complexes) with boundary.
-orientable. An orientation is also defined for manifolds (Poincaré complexes) with boundary.
References
| [1] | B.A. Dubrovin, A.T. Fomenko, S.P. Novikov, "Modern geometry" , 1–2 , Springer (1984–1985) (Translated from Russian) |
| [2] | , Introduction to topology , Moscow (1980) (In Russian) |
| [3] | V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian) |
| [4] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [5] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [6] | A. Dold, "Relations between ordinary and extraordinary homology" , Colloq. Algebraic Topology, August 1–10, 1962 , Inst. Math. Aarhus Univ. (1962) pp. 2–9 |
| [7] | J.P. May, "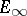 -ring spaces and -ring spaces and  -ring spectra" , Lect. notes in math. , 577 , Springer (1977) -ring spectra" , Lect. notes in math. , 577 , Springer (1977) |
| [8] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [9] | G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) |
| [10] | Yu.B. Rudyak, "On the orientability of spherical, topological, and piecewise-linear fibrations in complex 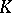 -theory" Soviet Math. Dokl. , 37 : 1 (1988) pp. 283–286 Dokl. Akad. Nauk SSSR , 298 : 6 (1988) pp. 1338–1340 -theory" Soviet Math. Dokl. , 37 : 1 (1988) pp. 283–286 Dokl. Akad. Nauk SSSR , 298 : 6 (1988) pp. 1338–1340 |
Comments
References
| [a1] | M.W. Hirsch, "Differential topology" , Springer (1976) |
Orientation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orientation&oldid=14762